题目内容
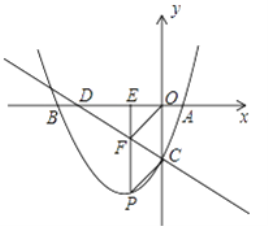
【题目】如图,已知抛物线y=ax2+ ![]() x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣
x+c与x轴交于A,B两点,与y轴交于丁C,且A(2,0),C(0,﹣4),直线l:y=﹣ ![]() x﹣4与x轴交于点D,点P是抛物线y=ax2+
x﹣4与x轴交于点D,点P是抛物线y=ax2+![]() x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
x+c上的一动点,过点P作PE⊥x轴,垂足为E,交直线l于点F.
(1)试求该抛物线表达式;
(2)求证:点C在以AD为直径的圆上;
(3)是否存在点P使得四边形PCOF是平行四边形,若存在求出P点的坐标,不存在请说明理由。
【答案】(1)y= ![]() x2+
x2+ ![]() x﹣4;(2)见解析;(3)(﹣
x﹣4;(2)见解析;(3)(﹣![]() ,﹣
,﹣![]() )或(﹣8,﹣4).
)或(﹣8,﹣4).
【解析】试题分析:(1)将点A和点C的坐标代入抛物线的解析式可得到关于a、c的方程组,然后解方程组求得a、c的值即可;
(2)求出D点坐标,根据两点间距离公式分别求出AD、AC、CD的长,然后根据勾股定理的逆定理证明出△ADC为直角三角形即可得出结论;
(3)设P(m,![]() m2+
m2+![]() m-4),则F(m,-
m-4),则F(m,-![]() m-4),则PF=-
m-4),则PF=-![]() m2-
m2-![]() m,当PF=OC时,四边形PCOF是平行四边形,然后依据PF=OC列方程求解即可.
m,当PF=OC时,四边形PCOF是平行四边形,然后依据PF=OC列方程求解即可.
试题解析:
(1)解:由题意得: ![]() ,解得:
,解得: ![]() ,
,
∴抛物线的表达式为y= ![]() x2+
x2+ ![]() x﹣4.
x﹣4.
(2)证明:把y=0代入y=﹣ ![]() x﹣4得:﹣
x﹣4得:﹣ ![]() x﹣4=0,
x﹣4=0,
解得:x=﹣8.
∴D(﹣8,0).
∴OD=8.
∵A(2,0),C(0,﹣4),∴AD=2﹣(﹣8)=10.
由两点间的距离公式可知:AC2=22+42=20,DC2=82+42=80,AD2=100,
∴AC2+CD2=AD2 .
∴△ACD是直角三角形,且∠ACD=90°,
∴点C在以AD为直径的圆上;
(3)解:设P(m, ![]() m2+
m2+ ![]() m﹣4),则F(m,﹣
m﹣4),则F(m,﹣ ![]() m﹣4).
m﹣4).
∴PF=(﹣ ![]() m﹣4)﹣(
m﹣4)﹣( ![]() m2+
m2+ ![]() m﹣4)=﹣
m﹣4)=﹣ ![]() m2﹣
m2﹣ ![]() m.
m.
∵PE⊥x轴,∴PF∥OC.
∴PF=OC时,四边形PCOF是平行四边形.
∴﹣ ![]() m2﹣
m2﹣ ![]() m=4,解得:m=﹣
m=4,解得:m=﹣ ![]() 或m=﹣8.
或m=﹣8.
当m=﹣ ![]() 时,
时, ![]() m2+
m2+ ![]() m﹣4=﹣
m﹣4=﹣ ![]() ,
,
当m=﹣8时, ![]() m2+
m2+ ![]() m﹣4=﹣4.
m﹣4=﹣4.
∴点P的坐标为(﹣ ![]() ,﹣
,﹣ ![]() )或(﹣8,﹣4).
)或(﹣8,﹣4).

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】有这样一对数,如下表,第![]() 个数比第n个数大2(其中n是正整数)
个数比第n个数大2(其中n是正整数)
第1个 | 第2个 | 第3个 | 第4个 | 第5个 | …… |
a | b | c |
(1)第5个数表示为______;第7个数表示为_______.
(2)若第10个数是5,第11个数是8,第12个数为9,则a=______,b=_____,c=______.
(3)第2019个数可表示为________.
【题目】某公司从2014年开始投入技术改进资金,经技术改进后,其产品的成本不断降低,具体数据如下表:
年 度 | 2013 | 2014 | 2015 | 2016 |
投入技改资金 | 2.5 | 3 | 4 | 4.5 |
产品成本 | 7.2 | 6 | 4.5 | 4 |
(1)请你认真分析表中数据,从一次函数和反比例函数中确定哪一个函数能表示其变化规律,给出理由,并求出其解析式;
(2)按照这种变化规律,若2017年已投入资金5万元.
①预计生产成本每件比2016年降低多少万元?
②若打算在2017年把每件产品成本降低到3.2万元,则还需要投入技改资金多少万元?(结果精确到0.01万元).