题目内容
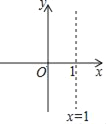
【题目】在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c).
(1)当c=﹣3时,点(x1,y1)在抛物线y=x2﹣2x+c上,求y1的最小值;
(2)若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA=![]() OB,求抛物线的解析式;
OB,求抛物线的解析式;
(3)当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.
【答案】(1)-4(2)y=x2﹣2x+![]() 或y=x2﹣2x﹣8(3)当﹣3<c<0时,抛物线与x轴有且只有一个公共点
或y=x2﹣2x﹣8(3)当﹣3<c<0时,抛物线与x轴有且只有一个公共点
【解析】
(1)根据二次函数的性质,求出顶点的纵坐标即可解决问题;
(2)分两种情形①当点A、B都在原点的右侧时,如解图1,②当点A在原点的左侧,点B在原点的右侧时,如解图2,分别求解即可;
(3)把问题转化为不等式即可解决问题;
(1)当c=﹣3时,抛物线为y=x2﹣2x﹣3,
∴抛物线开口向上,有最小值,
∴y最小值=![]() =﹣4,
=﹣4,
∴y1的最小值为﹣4;
(2)抛物线与x轴有两个交点,
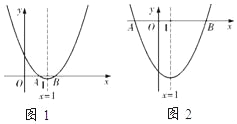
①当点A、B都在原点的右侧时,如解图1,
设A(m,0),
∵OA=![]() OB,
OB,
∴B(2m,0),
∵二次函数y=x2﹣2x+c的对称轴为x=1,
由抛物线的对称性得1﹣m=2m﹣1,解得m=![]() ,
,
∴A(![]() ,0),
,0),
∵点A在抛物线y=x2﹣2x+c上,
∴0=![]() ﹣
﹣![]() +c,解得c=
+c,解得c=![]() ,
,
此时抛物线的解析式为y=x2﹣2x+![]() ;
;
②当点A在原点的左侧,点B在原点的右侧时,如解图2,
设A(﹣n,0),
∵OA=![]() OB,且点A、B在原点的两侧,
OB,且点A、B在原点的两侧,
∴B(2n,0),
由抛物线的对称性得n+1=2n﹣1,
解得n=2,
∴A(﹣2,0),
∵点A在抛物线y=x2﹣2x+c上,
∴0=4+4+c,解得c=﹣8,
此时抛物线的解析式为y=x2﹣2x﹣8,
综上,抛物线的解析式为y=x2﹣2x+![]() 或y=x2﹣2x﹣8;
或y=x2﹣2x﹣8;
(3)∵抛物线y=x2﹣2x+c与x轴有公共点,
∴对于方程x2﹣2x+c=0,判别式b2﹣4ac=4﹣4c≥0,
∴c≤1.
当x=﹣1时,y=3+c;当x=0时,y=c,
∵抛物线的对称轴为x=1,且当﹣1<x<0时,抛物线与x轴有且只有一个公共点,
∴3+c>0且c<0,解得﹣3<c<0,
综上,当﹣3<c<0时,抛物线与x轴有且只有一个公共点.