题目内容
【题目】在平面直角坐标系xOy中，正方形A1B1C1O、A2B2C2B1、A3B3C3B2 ， …，按图所示的方式放置．点A1、A2、A3 ， …和点B1、B2、B3 ， …分别在直线y=kx+b和x轴上．已知C1（1，﹣1），C2（ 
， 
），则点A3的坐标是 ． 
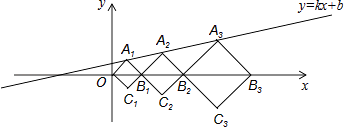
【答案】（ 
,
）
【解析】解：连接A1C1，A2C2，A3C3，分别交x轴于点E、F、G，
∵正方形A1B1C1O、A2B2C2B1、A3B3C3B2，
∴A1与C1关于x轴对称，A2与C2关于x轴对称，A3与C3关于x轴对称，
∵C1（1，﹣1），C2（ 
， 
），
∴A1（1，1），A2（ ， 
），
∴OB1=2OE=2，OB2=OB1+2B1F=2+2×（ ﹣2）=5，
将A1与A2的坐标代入y=kx+b中得： 
，
解得： 
，
∴直线解析式为y= 
x+ 
，
设B2G=A3G=t，则有A3坐标为（5+t，t），
代入直线解析式得：b= （5+t）+ ，
解得：t= ，
∴A3坐标为（ ， ）．
故答案是：（ ， ）．
练习册系列答案
快捷英语周周练系列答案
相关题目
【题目】某工厂计划生产A、B两种产品共10件，其生产成本和利润如下表．
A种产品 | B种产品 | |
成本（万元/件） | 2 | 5 |
利润（万元/件） | 1 | 3 |
（1）若工厂计划获利14万元，问A，B两种产品应分别生产多少件？
（2）若工厂计划投入资金不多于44万元，且获利多于14万元，求工厂的最大利润？
