题目内容
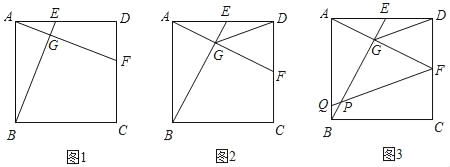
【题目】如图，在△ABC中，点D、E分别为BC、AD的中点，EF=2FC，若△ABC的面积为12 cm2，则△BEF的面积为（ ）
A.
B.
C.
D.
【答案】C
【解析】
由点D是BC的中点，可得△ABD的面积=△ACD的面积=
△ABC，由E是AD的中点，得出△ABE的面积=△D BE的面积=
△ABC的面积，进而得出△BCE的面积=△ABC的面积，再利用EF=2FC，求出△BEF的面积.
点D是BC的中点，
△ABD的面积=△ACD的面积=△ABC的面积= 6，
E是AD的中点，△ABE的面积=△DBE的面积=△ABC的面积= 3，
△ACE的面积=△DCE的面积=△ABC的面积= 3，
△BCE的面积=△ABC的面积= 6,
EF= 2FC，△BEF的面积=
6=4.
故选C
练习册系列答案
相关题目
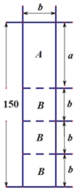
【题目】装饰公司为小明家设计电视背景墙时需要A、B型板材若干块，A型板材规格是ab，B型板材规格是bb．现只能购得规格是150b的标准板材．（单位：cm）
（1）若设a60cm，b30cm．一张标准板材尽可能多的裁出A型、B型板材，共有下表三种裁法，下图是裁法一的裁剪示意图．
裁法一 | 裁法二 | 裁法三 | |
A型板材块数 | 1 | 2 | 0 |
B型板材块数 | 3 | m | n |
则上表中， m=___________， n=__________；
（2）为了装修的需要，小明家又购买了若干C型板材，其规格是aa，并做成如下图的背景墙．请写出下图中所表示的等式：__________；
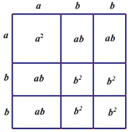
(3)若给定一个二次三项式2a25ab3b2，试用拼图的方式将其因式分解．（请仿照（2）在几何图形中标上有关数量）
