题目内容
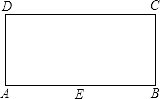
【题目】四边形ABCD是边长为4的正方形,点E在边AD所在直线上,连接CE,以CE为边,作正方形CEFG(C、E、F、G按顺时针排列),连接BF.
(1)如图1,当点E与点A重合时,请直接写出BF的长;
(2)如图2,当点E在线段AD上时,AE=1,求BF的长;
(3)若BG3![]() ,请求出此时AE的长.
,请求出此时AE的长.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)AE的长为1或2+
;(3)AE的长为1或2+![]() .
.
【解析】
(1)作FH⊥AB于H,由AAS证明△EFH≌△CED,得出FH=CD=4,AH=AD=4,求出BH=AB+AH=8,由勾股定理即可得出答案;
(2)过F作FH⊥AD交AD的延长线于点H,作FM⊥AB于M,则FM=AH,AM=FH,①同(1)得:△EFH≌△CED,得出FH=DE=3,EH=CD=4即可;
②求出BM=AB+AM=7,FM=AE+EH=5,由勾股定理即可得出答案;
(3)分两种情况:①当点E在边AD的左侧时,过F作FH⊥AD交AD的延长线于点H,交BC延长线于K,同(1)得:△EFH≌△CED,得出FH=DE=4+AE,EH=CD=4,得出FK=8+AE,在Rt△BFK中,BK=AH=EH-AE=4-AE,由勾股定理得出方程,解方程即可;
②当点E在边AD的右侧时,过F作FH⊥AD交AD的延长线于点H,交BC延长线于K,同理得AE的长.
(1)作FH⊥AB于H,如图1所示:

则∠FHE=90°,
∵四边形ABCD和四边形CEFG是正方形,
∴AD=CD=4,EF=CE,∠ADC=∠DAH=∠BAD=∠CEF=90°,
∴∠FEH=∠CED,
在△EFH和△CED中,
 ,
,
∴△EFH≌△CED(AAS),
∴FH=CD=4,AH=AD=4,
∴BH=AB+AH=8,
∴BF=![]() ;
;
(2)过F作FH⊥AD交AD的延长线于点H,作FM⊥AB于M,如图2所示:

则FM=AH,AM=FH,
①∵AD=4,AE=1,∴DE=3,
同(1)得:△EFH≌△CED(AAS),
∴FH=DE=3,EH=CD=4,
∴BM=AB+AM=4+3=7,FM=AE+EH=5,
∴BF=![]() ;
;
(3)分两种情况:
①当点E在边AD的左侧时,过F作FH⊥AD交AD于点H,交BC延长线于K.如图3所示:

同(1)得:△EFH≌△CED,
∴FH=DE=AE+4,EH=CD=4,
∴FK=8+AE,在Rt△BFK中,BK=AH=EH-AE=4-AE,
由勾股定理得:(4-AE)2+(8+AE)2=(3![]() )2,
)2,
解得:AE=1或AE=-5(舍去),
∴AE=1;
②当点E在边AD的右侧时,过F作FH⊥AD交AD的延长线于点H,交BC延长线于K,如图4所示:

同理得:AE=2+![]() 或2-
或2-![]() (舍去).
(舍去).
③当点E在AD上时,可得:(8-AE)2+(4+AE)2=90,
解得AE=5或-1,
5>4不符合题意.
综上所述:AE的长为1或2+![]() .
.

【题目】白色污染( Whitepollution)是人们对难降解的塑料垃圾(多指塑料袋)污染环境现象的一种形象称谓.为了让全校同学感受丢弃塑料袋对环境的影响,小彬随机抽取某小区![]() 户居民,记录了这些家庭
户居民,记录了这些家庭![]() 年某个月丢弃塑料袋的数量(单位:个)
年某个月丢弃塑料袋的数量(单位:个)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
请根据上述数据,解答以下问题:

(1)小彬按“组距为![]() ”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
”列出了如下的频数分布表(每组数据含最小值不含最大值),请将表中空缺的部分补充完整,并补全频数直方图;
分组 | 划记 | 频数 |
| _______ | ________ |
|
|
|
| _______ | ________ |
|
|
|
合计 | / |
|
(2)根据(1)中的直方图可以看出,这![]() 户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
户居民家这个月丢弃塑料袋的个数在 组的家庭最多;(填分组序号)
(3)根据频数分布表,小彬又画出了如图所示的扇形统计图.请将统计图中各组占总数的百分比填在图中,并求出![]() 组对应的扇形圆心角的度数;
组对应的扇形圆心角的度数;
(4)若该小区共有![]() 户居民家庭,请你估计每月丢弃的塑料袋数量不小于
户居民家庭,请你估计每月丢弃的塑料袋数量不小于![]() 个的家庭个数.
个的家庭个数.