题目内容
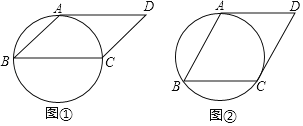
【题目】如图，AB为半圆O的直径，直线CE与半圆O相切于点C，点D是
的中点，CB=6，四边形ABCD的面积为
AC，则圆心O到直线CE的距离是____．
【答案】
．
【解析】
接OD交AC于H，连接OC由垂径定理可得AH=HC，根据三角形中位线定理可得OH=
BC，由S四边形ABCD=S△ADC+S△ABC求出DH长，易知OD长，由切线的性质可得圆心O到直线CE的距离为OC长.
解：如图，连接OD交AC于H，连接OC．
∵
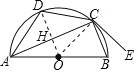
，∴OD⊥AC，∴AH=HC．
∵OA=OB，∴OH=BC=3．
∵S四边形ABCD=S△ADC+S△ABC，∴ACDH+ACBC=3
AC，∴DH+6=6，
∴DH=6﹣6，∴OD=DH+OH=6﹣3．
∵EC是切线，∴OC⊥EC，∴圆心O到直线CE的距离为6﹣3．
故答案为：6﹣3．
练习册系列答案
相关题目
