题目内容
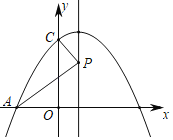
【题目】如图,抛物线y=﹣![]() x2+
x2+![]() x+3与x轴交于点A,B(点A在点B的左边),交y轴于点C,点P为抛物线对称轴上一点.则△APC的周长最小值是_____.
x+3与x轴交于点A,B(点A在点B的左边),交y轴于点C,点P为抛物线对称轴上一点.则△APC的周长最小值是_____.
【答案】![]() +5
+5
【解析】
先连接AP、AC、BC,根据两点之间,线段最短得到△APC周长最小=BC+AC,根据二次函数解析式,求出A、B、C三点坐标,用勾股定理求出BC、AC即可.
解:如图,连接AP、AC、BC,
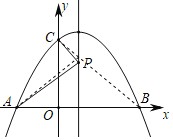
由线段垂直平分线性质,得AP=BP,
∴△APC周长=AP+PC+AC=BP+PC+AC,
∴当BC与对称轴交点则为点P时,
△APC周长=BP+PC+AC=BC+AC最小,
抛物线y=-![]() x2+
x2+![]() x+3中,令y=0,解得x=4或x=-2;令x=0,解得y=3,
x+3中,令y=0,解得x=4或x=-2;令x=0,解得y=3,
∴A(-2,0),B(4,0),C(0,3),
∴OA=2,OB=4,OC=3,
在Rt△AOC中,有AC=![]() =
=![]() ,
,
在Rt△BOC中,有BC=![]() =5,
=5,
∴△APC的周长的最小值为:![]() +5,
+5,
故答案为![]() +5.
+5.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
【题目】将正偶数按下表排成5列:
第一列 | 第二列 | 第三列 | 第四列 | 第五列 | |
第一行 | 2 | 4 | 6 | 8 | |
第二行 | 16 | 14 | 12 | 10 | |
第三行 | 18 | 20 | 22 | 24 | |
第四行 | 32 | 30 | 28 | 26 | |
…… |
根据上面规律,2020应在( )
A.125行,3列B.125行,2列C.253行,2列D.253行,3列