МвДҝДЪИЭ
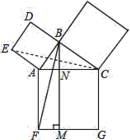
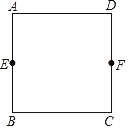
ЎҫМвДҝЎҝИзНјЈ¬ҫШРОABCDЦРЈ¬AB=8Ј¬BC=6Ј¬Ҫ«ҙЛҫШРОИЖөгBЛіКұХл·ҪПтРэЧӘҰИЈЁ0ЈјҰИЈј180ЎгЈ©өГөҪҫШРОA1BC1D1Ј¬ЦұПЯBA1ЎўC1D1·ЦұрУлЦұПЯCDПаҪ»УЪөгEЎўFЈ®
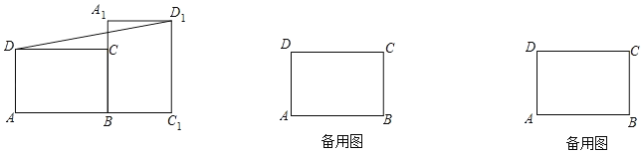
ЈЁ1Ј©ИфҙЛҫШРОИЖөгBЛіКұХл·ҪПтРэЧӘ90ЎгЈ¬ЗуDD1өДіӨЈ»
ЈЁ2Ј©ФЪРэЧӘ№эіМЦРЈ¬өгDЎўA1ЎўD1Иэөг№ІПЯКұЈ¬ЗуЎчBCEөДГж»эЈ»
ЈЁ3Ј©ФЪҫШРОABCDРэЧӘөД№эіМЦРЈ¬КЗ·сҙжФЪДіёцО»ЦГК№өГТФBЎўEЎўFЎўD1ОӘ¶ҘөгөДЛДұЯРООӘЖҪРРЛДұЯРОЈҝИфҙжФЪЈ¬ЗуіцCFөДіӨЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
Ўҫҙр°ёЎҝЈЁ1Ј©DD1=![]() Ј»ЈЁ2Ј©SЎчBEC=
Ј»ЈЁ2Ј©SЎчBEC=![]() Ј»ЈЁ3Ј©CF=18Ј®
Ј»ЈЁ3Ј©CF=18Ј®
ЎҫҪвОцЎҝ
ЈЁ1Ј©СУіӨDCҪ»C1D1УЪHЈ¬АыУГҫШРОөДРФЦКҝЙөГDHәНHD1іӨЈ¬УЙ№ҙ№Й¶ЁАнЗуҪвјҙҝЙЈ»
ЈЁ2Ј©Б¬ҪУBDЈ¬УЙHL¶ЁАнҝЙЦӨЎчBDA1ЎХЎчDBCЈ¬ЙиDE=BE=xЈ¬ФЪRtЎчBCEЦРЈ¬УЙ№ҙ№Й¶ЁАнҝЙЦӘDEіӨЈ¬ТЧЦӘCEіӨЈ¬ёщҫЭГж»э№«КҪЗуҪвјҙҝЙЈ»
ЈЁ3Ј©УЙ№ҙ№Й¶ЁАнҝЙөГEFіӨЈ¬ёщҫЭtanЎПCEB=tanЎПEBD1өДұнКҫҝЙөГECіӨЈ¬ТЧЗуCF.
ҪвЈәЈЁ1Ј©ИзНј1ЦРЈ¬СУіӨDCҪ»C1D1УЪHЈ®
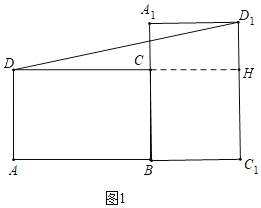
ЎЯЛДұЯРОABCDЈ¬ЛДұЯРОA1BC1D1КЗҫШРОЈ¬ЎаЎПA=ЎПADH=ЎПAC1H=90ЎгЈ¬ЎаЛДұЯРОADHC1КЗҫШРОЈ¬ЎаDH=AC=8+6=14Ј¬HC1=AD=6Ј¬ЎПDHC1=ЎПDHD1=90ЎгЈ¬ЎаHD1=8©Ғ6=2Ј¬ЎаDD1=![]() =
=![]() =
=![]() Ј®
Ј®
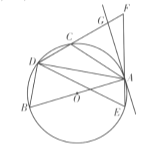
ЈЁ2Ј©ИзНј2ЦРЈ¬Б¬ҪУBDЈ®
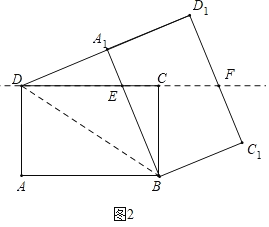
ЎЯЎПDA1B=ЎПDCB=90ЎгЈ®BD=DBЈ¬BA1=DCЈ¬ЎаЎчBDA1ЎХЎчDBCЈЁHLЈ©Ј¬ЎаЎПDBA1=ЎПBDCЈ¬ЎаED=EBЈ¬ЙиDE=BE=xЈ¬
ФЪRtЎчBCEЦРЈ¬ЎЯBE2=EC2+BC2Ј¬Ўаx2=ЈЁ8©ҒxЈ©2+62Ј¬Ўаx=![]() Ј¬ЎаEC=8©Ғ
Ј¬ЎаEC=8©Ғ![]() =
=![]() Ј¬ЎаSЎчBEC=
Ј¬ЎаSЎчBEC=![]() BCEC=
BCEC=![]() ЎБ6ЎБ
ЎБ6ЎБ![]() =
=![]() Ј®
Ј®
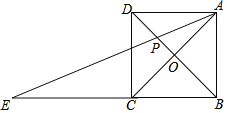
ЈЁ3Ј©ИзНј3ЦРЈ¬ҙжФЪЈ®

ЎЯЛДұЯРОBD1FEКЗЖҪРРЛДұЯРОЈ¬ЎаEF=BD1=![]() =10Ј®
=10Ј®
ЎЯECЎОBD1Ј¬ЎаЎПCEB=ЎПA1BD1Ј¬ЎаtanЎПCEB=tanЎПEBD1Ј¬Ўа![]() Ј¬Ўа
Ј¬Ўа![]() Ј¬ЎаEC=8Ј¬ЎаCF=EC+EF=8=10=18Ј®
Ј¬ЎаEC=8Ј¬ЎаCF=EC+EF=8=10=18Ј®

 ГыРЈҝОМГПөБРҙр°ё
ГыРЈҝОМГПөБРҙр°ёЎҫМвДҝЎҝОӘБЛКөПЦО°ҙуөДЗҝ№ъёҙРЛГОЈ¬И«Йз»б¶јФЪҝӘХ№ЙЁәЪіэ¶сЧЁПо¶·ХщЈ¬ДіЗшОӘБЛҪвёчѧУАПКҰ¶ФЙЁәЪіэ¶сУҰЦӘУҰ»бЦӘК¶өДХЖОХЗйҝцЈ¬¶ФјЧЎўТТБҪёцѧУёч180ГыАПКҰҪшРРБЛІвКФЈ¬ҙУЦРёчЛж»ъійИЎ30ГыҪМКҰөДіЙјЁ(°Щ·ЦЦЖ)Ј¬Іў¶ФіЙјЁЈЁөҘО»Јә·ЦЈ©ҪшРРХыАнЎўГиКцәН·ЦОцЈ¬ёшіцБЛІҝ·ЦіЙјЁРЕПўЈ®

јЧРЈІОУлІвКФөДАПКҰіЙјЁФЪ96ЎЬxЈј98ХвТ»ЧйөДКэҫЭКЗЈә96Ј¬96.5Ј¬97Ј¬97.5Ј¬97Ј¬96.5Ј¬97.5Ј¬96Ј¬96.5Ј¬96.5Ј¬јЧЎўТТБҪРЈІОУлІвКФөДАПКҰіЙјЁөДЖҪҫщКэЎўЦРО»КэЎўЦЪКэИзПВұнЈә
ѧУ | ЖҪҫщКэ | ЦРО»Кэ | ЦЪКэ |
јЧРЈ | 96.35 | m | 99 |
ТТРЈ | 95.85 | 97.5 | 99 |
ёщҫЭТФЙПРЕПўЈ¬»ШҙрПВБРОКМвЈә
ЈЁ1Ј©mЈҪ________Ј»
ЈЁ2Ј©ФЪҙЛҙОЛж»ъійСщІвКФЦРЈ¬јЧРЈөДНхАПКҰәНТТРЈөДАоАПКҰіЙјЁҫщОӘ97·ЦЈ¬ФтЛыГЗФЪёчЧФѧУІОУлІвКФөДАПКҰЦРіЙјЁөДГыҙОПаұИҪПёьҝҝЗ°өДКЗ________ЈЁСЎМоНх»тАоЈ©АПКҰЈ¬ЗлРҙіцАнУЙЈ»
ЈЁ3Ј©ФЪҙЛҙОЛж»ъІвКФЦРЈ¬ТТРЈ96·ЦТФЙПЈЁә¬96·ЦЈ©өДЧЬИЛКэұИјЧРЈ96·ЦТФЙП(ә¬96·Ц)өДЧЬИЛКэөД2ұ¶ЙЩ100ИЛЈ¬КФ№АјЖТТРЈ96·ЦТФЙПЈЁә¬96·ЦЈ©өДЧЬИЛКэЈ®