题目内容
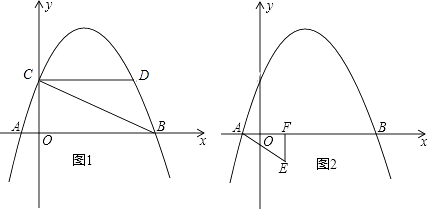
【题目】已知矩形ABCD,点P为BC边上一动点,连接AP,将线段AP绕P点顺时针旋转90°,点A恰好落在直线CD上点E处.
(1)如图1,点E在线段CD上,求证:AD+DE=2AB;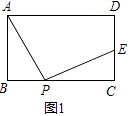
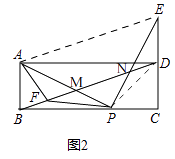
(2)如图2,点E在线段CD的延长线上,且点D为线段CE的中点,在线段BD上取点F,连接AF、PF,若AF=AB.求证:∠APF=∠ADB.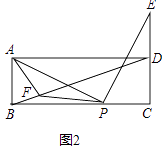
(3)如图3,点E在线段CD上,连接BD,若AB=2,BD∥PE,则DE= . (直接写出结果)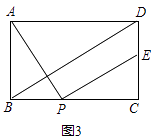
【答案】
(1)
解:∵四边形ABCD是矩形,
∴∠ABC=∠BCD=90°,
∴∠BAP+∠APB=90°,
∵∠APE=90°,
∴∠APB+∠CPE=90°,
∴∠BAP=∠CPE,
在△ABP和△PCE中, 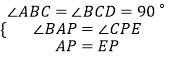 ,
,
∴△ABP≌△PCE,
∴AB=PC=CD,BP=CE,
∴AD+DE=BC+DE=BP+PC+DE=CE+CP+DE=CP+CD=2AB
(2)
解:如图,
∵AB=AF,
∴∠ABF=∠AFB,
∵AB∥DC,
∴∠ABF=∠BDC,
∴∠AFB=∠BDC,
∴∠AFD=∠EDF,
∵AB=CD=DE,AB∥CD,
∴四边形ABDE是平行四边形,
∴BD∥AE,
∵PA=PE,∠APE=90°,
∴∠PAE=∠PEA=45°,
∴∠PMN=∠PNM=45°,
∵BD∥AE,
∴∠FAE+∠AFD=180°,∠FDE+∠AED=180°,
∵∠AFD=∠EDF,
∴∠FAE=∠DEA,
∵∠PAE=∠PEA,
∴∠FAP=∠DEP,
在△APF和△EPD中, 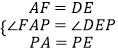 ,
,
∴△APF≌△EPD,
∴∠AFP=∠DEP,
∵∠AFD=∠EDF,
∴∠PFD=∠PDF,
在Rt△PCD中,PC=PD,
∴∠CDP=45°,
∴∠ADP=45°,
∴∠ADB=45°﹣∠PDF=45°﹣∠PFD,
∵∠AMB=∠PFD+∠APF=45°,
∴∠APF=45°﹣∠PFD,
∴∠APF=∠ADB
(3)3﹣ ![]()
【解析】解:(3)由(1)知,△ABP≌△PCE,
∴PC=AB=2,由(1)知,AD+DE=2AB=4,
∴AD=4﹣DE,
∵DB∥PE,
∴△CPE∽△CBD,
∴ ![]() ,
,
∵CB=AD=4﹣DE,CD=AB=2,CE=CD﹣DE=2﹣DE,
∴ ![]() ,
,
∴DE=3+ ![]() (由于点E在线段CD上,且CD=2,所以舍去)或DE=3﹣
(由于点E在线段CD上,且CD=2,所以舍去)或DE=3﹣ ![]() ,
,
即:DE=3﹣ ![]() ,
,
所以答案是:3﹣ ![]() .
.
【考点精析】解答此题的关键在于理解三角形的外角的相关知识,掌握三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角,以及对相似三角形的判定的理解,了解相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

 口算题天天练系列答案
口算题天天练系列答案