题目内容
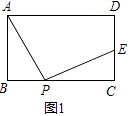
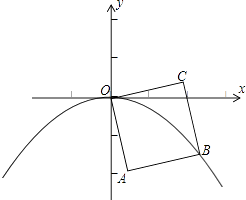
【题目】如图1抛物线y=ax2+bx+c过 A（﹣1，0）、B（4，0）、C（0，2）三点．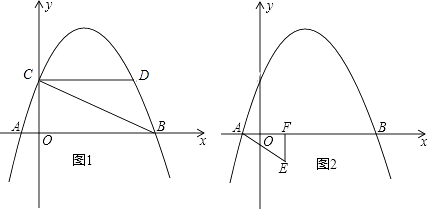
（1）求抛物线解析式；
（2）点C，D关于抛物线对称轴对称，求△BCD的面积；
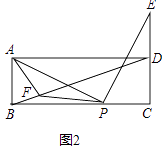
（3）如图2，过点E（1，﹣1）作EF⊥x轴于点F，将△AEF绕平面内某点旋转180°得△MNQ（点M、N、Q分别与A、E、F对应）使得M、N在抛物线上，求M、N的坐标．
【答案】
（1）
解：抛物线y=ax2+bx+c过 A（﹣1，0）、B（4，0）、C（0，2）三点，
∴可设抛物线解析式为y=a（x+1）（x﹣4），
把C（0，2）代入得2=a（0+1）（0﹣4），解得a=﹣ 
，
∴抛物线解析式为y=﹣ （x+1）（x﹣4）=﹣ x2+ 
x+2
（2）
解：抛物线对称轴为x=﹣ 
=﹣ 
= ，
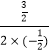∵点 C（0，2），D关于抛物线对称轴对称，
∴D（3，2），
∴CD=3，
∴S△BCD= CDOC= ×3×2=3
（3）
解：∵A（﹣1，0），E（1，﹣1），EF⊥x轴于点F，
∴AF=2，EF=1
如图2，由旋转知△MNQ≌△AEF，
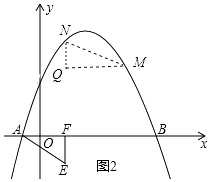
∴MQ=AF=2，NQ=EF=1，
且MQ∥x轴，NQ⊥x轴，
设N（m，n），则M（m+2，n﹣1），
代入抛物线解析式y=﹣ x2+ x+2，
得 
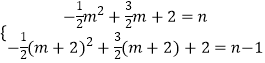，解得 
，
∴M（3，2），N（1，3）
【解析】（1）由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；（2）由抛物线解析式可求得抛物线对称轴，可求得D点坐标，则可求得△BCD的面积；（3）由旋转知△MNQ≌△AEF，设N点坐标为（m，n），则可表示出M点坐标，把M、N的坐标代入抛物线解析式可得到关于m、n的方程组，可求得m、n的值，则可求得M、N的坐标．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．
