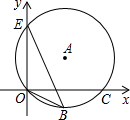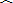题目内容
如图,在△ABC中,∠B=30°,以边AB的中点O为圆心,BO长为半径作⊙O,恰好过顶点C.在半圆AB上取点D,连接CD.
(1)∠ACB的度数为______°,理由是______.
(2)在半圆AB上取中点D,连接CD.若AC=6,补全图形并求CD的长.

(1)∠ACB的度数为______°,理由是______.
(2)在半圆AB上取中点D,连接CD.若AC=6,补全图形并求CD的长.

(1)∵AB是⊙O的直径,⊙O过点C,
∴∠ACB=90°(直径所对的圆周角是直角).
(2)分两种情况讨论:
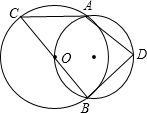
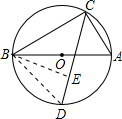 ①C、D两点在直径AB异侧,连接BD,过B作BE⊥CD于E.
①C、D两点在直径AB异侧,连接BD,过B作BE⊥CD于E.
在△ABC中,∵∠ACB=90°,∠ABC=30°,AC=6,
∴AB=2AC=12,BC=
AC=6
.
∵在半圆AB上取中点D,
∴∠BCD=45°,
∴△BCE是等腰直角三角形,
∴BE=CE=
BC=3
.
在△BDE中,∵∠BED=90°,∠D=∠A=60°,
∴DE=
BE=3
,
∴CD=CE+DE=3
+3
;
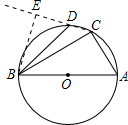 ②C、D两点在直径AB同侧,
②C、D两点在直径AB同侧,
连接BD,过B作BE⊥CD于E.
在△ABC中,∵∠ACB=90°,∠ABC=30°,AC=6,
∴AB=2AC=12,BC=
AC=6
.
∵在半圆AB上取中点D,
∴∠BCD=45°,
∴△BCE是等腰直角三角形,
∴BE=CE=
BC=3
.
在△BDE中,∵∠BED=90°,∠BDE=∠A=60°,
∴DE=
BE=3
,
∴CD=CE-DE=3
-3
.
故答案为:90,直径所对的圆周角是直角.
∴∠ACB=90°(直径所对的圆周角是直角).
(2)分两种情况讨论:
 ①C、D两点在直径AB异侧,连接BD,过B作BE⊥CD于E.
①C、D两点在直径AB异侧,连接BD,过B作BE⊥CD于E.在△ABC中,∵∠ACB=90°,∠ABC=30°,AC=6,
∴AB=2AC=12,BC=
| 3 |
| 3 |
∵在半圆AB上取中点D,
∴∠BCD=45°,
∴△BCE是等腰直角三角形,
∴BE=CE=
| ||
| 2 |
| 6 |
在△BDE中,∵∠BED=90°,∠D=∠A=60°,
∴DE=
| ||
| 3 |
| 2 |
∴CD=CE+DE=3
| 6 |
| 2 |
 ②C、D两点在直径AB同侧,
②C、D两点在直径AB同侧,连接BD,过B作BE⊥CD于E.
在△ABC中,∵∠ACB=90°,∠ABC=30°,AC=6,
∴AB=2AC=12,BC=
| 3 |
| 3 |
∵在半圆AB上取中点D,
∴∠BCD=45°,
∴△BCE是等腰直角三角形,
∴BE=CE=
| ||
| 2 |
| 6 |
在△BDE中,∵∠BED=90°,∠BDE=∠A=60°,
∴DE=
| ||
| 3 |
| 2 |
∴CD=CE-DE=3
| 6 |
| 2 |
故答案为:90,直径所对的圆周角是直角.

练习册系列答案
相关题目