题目内容
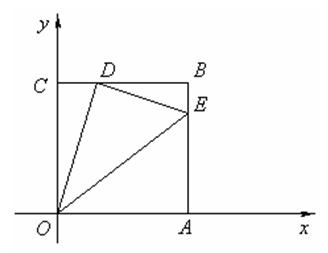
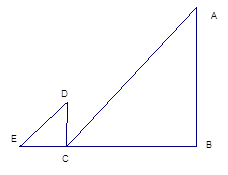
已知Rt△ABC中,AC=3,BC= 4,过直角顶点C作CA1⊥AB,垂足为A1,再过A1作A1C1⊥BC, 垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,…,这样一直做下去,得到了一组线段CA1,A1C1,C1A2,…,则CA1= , .
.
 .
.
由Rt△ABC中,AC=3,BC=4,利用勾股定理得AB=5,利用平行线的性质得出∠A1CA=∠C1A1C=∠A2C1A1=∠C2A2C1=…=∠C9A9C8,可证△C9A9C8∽△CBA,利用相似比求解
解:在Rt△ABC中,AC=3,BC=4,由勾股定理得AB=5,
∵CA1⊥AB,∠ACB=90°,
∴△A1CA∽△CBA
∴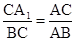 解得CA1=
解得CA1=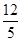
由平行线的性质,得∠A1CA=∠C9A9C8,
∴△C9A9C8∽△CBA,
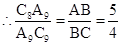
故答案为: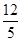 ,
,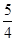
解:在Rt△ABC中,AC=3,BC=4,由勾股定理得AB=5,
∵CA1⊥AB,∠ACB=90°,
∴△A1CA∽△CBA
∴
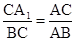 解得CA1=
解得CA1=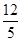
由平行线的性质,得∠A1CA=∠C9A9C8,
∴△C9A9C8∽△CBA,
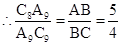
故答案为:
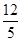 ,
,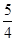

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

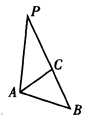
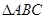 ∽
∽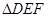 ,
,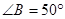 ,
,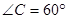 ,则
,则 的度数为 .
的度数为 .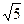 ,这个矩形的长宽各是多少?
,这个矩形的长宽各是多少?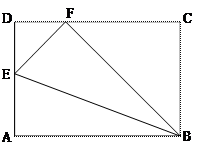
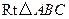 内接于
内接于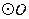 ,
,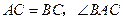 的平分线
的平分线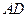 与
与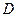 ,与
,与 交于点
交于点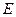 ,延长
,延长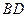 ,与
,与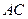 的延长线交于点
的延长线交于点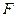 ,连接
,连接 是
是 的中点,连结
的中点,连结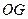 .
.
 ;
;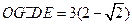 ,求
,求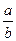 =
=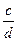 ,判断代数式
,判断代数式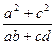 -
-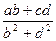 +1值的符号
+1值的符号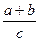 =
=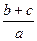 =
=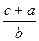 ,求
,求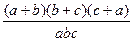 的值。
的值。