Question

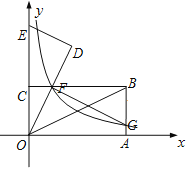
【题目】在如图平面直角坐标系中，矩形OABC的顶点B的坐标为（4，2），OA、OC分别落在x轴和y轴上，OB是矩形的对角线．将△OAB绕点O逆时针旋转，使点B落在y轴上，得到△ODE，OD与CB相交于点F，反比例函数y＝（x＞0）的图象经过点F，交AB于点G．

（1）求k的值和点G的坐标；

（2）连接FG，则图中是否存在与△BFG相似的三角形？若存在，请把它们一一找出来，并选其中一种进行证明；若不存在，请说明理由；

（3）在线段OA上存在这样的点P，使得△PFG是等腰三角形．请直接写出点P的坐标．

Answer 1

【答案】（1）k＝2，点G的坐标为（4，）；（2）△COF∽△BFG；△AOB∽△BFG；△ODE∽△BFG；△CBO∽△BFG，证明详见解析；（3）点P的坐标为（4﹣，0）或（，0）或（，0）．

【解析】

（1）证明△COF∽△AOB，则，求得：点F的坐标为（1，2），即可求解；

（2）△COF∽△BFG；△AOB∽△BFG；△ODE∽△BFG；△CBO∽△BFG．证△OAB∽△BFG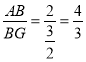：，，即可求解．

（3）分GF＝PF、PF＝PG、GF＝PG三种情况，分别求解即可．

解：（1）∵四边形OABC为矩形，点B的坐标为（4，2），

∴∠OCB＝∠OAB＝∠ABC＝90°，OC＝AB＝2，OA＝BC＝4，

∵△ODE是△OAB旋转得到的，即：△ODE≌△OAB，

∴∠COF＝∠AOB，∴△COF∽△AOB，

∴，∴＝，∴CF＝1，

∴点F的坐标为（1，2），

∵y＝（x＞0）的图象经过点F，

∴2＝，得k＝2，

∵点G在AB上，

∴点G的横坐标为4，

对于y＝，当x＝4，得y＝，

∴点G的坐标为（4，）；

（2）△COF∽△BFG；△AOB∽△BFG；△ODE∽△BFG；△CBO∽△BFG．

下面对△OAB∽△BFG进行证明：

∵点G的坐标为（4，），∴AG＝，

∵BC＝OA＝4，CF＝1，AB＝2，

∴BF＝BC﹣CF＝3，

BG＝AB﹣AG＝．

∴，．

∴，

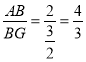∵∠OAB＝∠FBG＝90°，

∴△OAB∽△FBG．

（3）设点P（m，0），而点F（1，2）、点G（4，），

则FG2＝9+＝，PF2＝（m﹣1）2+4，PG2＝（m﹣4）2+，

当GF＝PF时，即＝（m﹣1）2+4，解得：m＝（舍去负值）；

当PF＝PG时，同理可得：m＝；

当GF＝PG时，同理可得：m＝4﹣；

综上，点P的坐标为（4﹣，0）或（，0）或（，0）．