Question

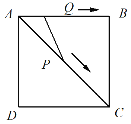
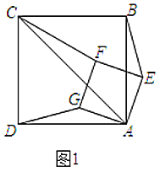
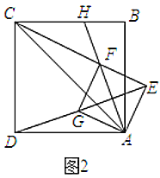
【题目】如图，正方形纸片的边长为，翻折，使两个直角顶点重合于对角线上一点分别是折痕，设，给出下列判断：

①当时，点是正方形的中心；

②当时，；

③当时，六边形面积的最大值是

④当时，六边形周长的值不变．

其中错误的是（ ）

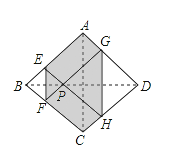
A.②③B.③④C.①④D.①②

Answer 1

【答案】A

【解析】

①由折叠的性质可知，和是等腰直角三角形，由此即可判断①的正误；

②由折叠的性质可知，，得出 ，同理，则可判断②的正误；

③利用六边形面积=正方形ABCD的面积-的面积-的面积得到函数关系式，从而即可确定最大值；

④利用六边形的周长为即可判断④的正误．

正方形纸片ABCD，翻折，使两个直角顶点重合于对角线上一点，

∴和是等腰直角三角形，

∴当时，重合点P是BD的中点，

∴点P是正方形ABCD的中心，

故①正确；

正方形纸片ABCD，翻折，使两个直角顶点重合于对角线上一点，

∴．

，

，

，

即，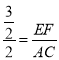

．

同理，．

，

故②错误；

六边形面积=正方形ABCD的面积-的面积-的面积，

∵，

∴六边形面积为：

∴六边形面积的最大值为3，

故③错误；

当时，

．

六边形的周长为

故④正确；

∴错误的是②③，

故选：A．