题目内容
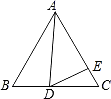
【题目】如图,在△ABC 中,AB=AC,CD是∠ACB的平分线,DE∥BC,交AC于点 E.
(1)求证:DE=CE.
(2)若∠CDE=35°,求∠A 的度数.

【答案】(1)见解析;(2) 40°.
【解析】
(1)根据角平分线的性质可得出∠BCD=∠ECD,由DE∥BC可得出∠EDC=∠BCD,进而可得出∠EDC=∠ECD,再利用等角对等边即可证出DE=CE;
(2)由(1)可得出∠ECD=∠EDC=35°,进而可得出∠ACB=2∠ECD=70°,再根据等腰三角形的性质结合三角形内角和定理即可求出∠A的度数.
(1)∵CD是∠ACB的平分线,∴∠BCD=∠ECD.
∵DE∥BC,∴∠EDC=∠BCD,∴∠EDC=∠ECD,∴DE=CE.
(2)∵∠ECD=∠EDC=35°,∴∠ACB=2∠ECD=70°.
∵AB=AC,∴∠ABC=∠ACB=70°,∴∠A=180°﹣70°﹣70°=40°.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】纸箱厂用如图1所示的长方形和正方形纸板,做成如图2所示的竖式与横式两种长方体形状的有底无盖纸盒.

(1)现有正方形纸板172张,长方形纸板330张.若要做两种纸盒共l00个,设做竖式纸盒x个.
①根据题意,完成以下表格:
| 竖式纸盒(个) | 横式纸盒(个) |
x | ||
正方形纸板(张) | 2(100-x) | |
长方形纸板(张) | 4x |
②按两种纸盒的数量分,有哪几种生产方案?
(2)若有正方形纸板112张,长方形纸板![]() 张,做成上述两种纸盒,纸板恰好用完.已知100<
张,做成上述两种纸盒,纸板恰好用完.已知100<![]() <110,则
<110,则![]() 的值是 .
的值是 .