题目内容
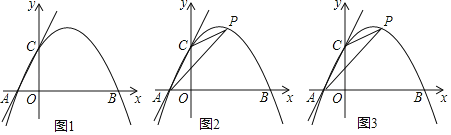
【题目】在平面直角坐标系中,O为坐标原点,过二次函数y=﹣x2+4x图象上的点A(3,3)作x轴的垂线交x轴于点B.
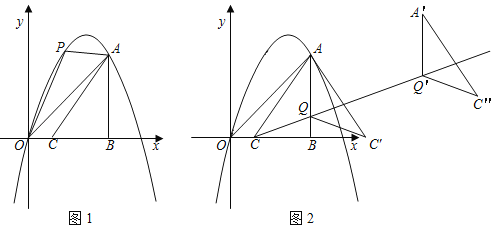
(1)如图1,P为线段OA上方抛物线上的一点,在x轴上取点C(1,0),点M、N为y轴上的两个动点,点M在点N的上方且MN=1.连接AC,当四边形PACO的面积最大时,求PM+MN![]() NO的最小值.
NO的最小值.
(2)如图2,点Q(3,1)在线段AB上,作射线CQ,将△AQC沿直线AB翻折,C点的对应点为C',将△AQC'沿射线CQ平移3![]() 个单位得△A'Q'C″,在射线CQ上取一点M,使得以A'、M、C″为顶点的三角形是等腰三角形,求M点的坐标.
个单位得△A'Q'C″,在射线CQ上取一点M,使得以A'、M、C″为顶点的三角形是等腰三角形,求M点的坐标.
【答案】(1)最小值为![]() ;(2)点M坐标为(7,3),(
;(2)点M坐标为(7,3),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(13,6),(10,
),(13,6),(10,![]() )
)
【解析】
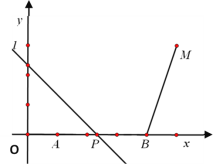
(1)把四边形PACO沿OA分成△OAP与△OAC,由于△OAC三边确定,面积为定值,故△OAP面积最大时四边形面积也最大.过点P作x轴垂线交OA于D,设点P横坐标为t,则能用t表示PD的长,进而得到△OAP关于t的二次函数关系式,用公式法可求得t![]() 时△OAP面积最大,即求得此时点P坐标.把点P向下平移1个单位得P',易证四边形MNP'P是平行四边形,所以PM=P'N.过点O作经过第二、四象限的直线l,并使直线l与x轴夹角为60°,过点N作NG⊥直线l于点G,则由30°角所对直角边等于斜边一半可知NG
时△OAP面积最大,即求得此时点P坐标.把点P向下平移1个单位得P',易证四边形MNP'P是平行四边形,所以PM=P'N.过点O作经过第二、四象限的直线l,并使直线l与x轴夹角为60°,过点N作NG⊥直线l于点G,则由30°角所对直角边等于斜边一半可知NG![]() NO.所以PM+MN
NO.所以PM+MN![]() NO可转化为P'N+NG+1,易得当点P'、N、G在同一直线上最小.把PD延长交直线l于点F,构造特殊Rt△P'FG和Rt△OEF,利用点P坐标和30°、60°的三角函数即可求得P'G的长.
NO可转化为P'N+NG+1,易得当点P'、N、G在同一直线上最小.把PD延长交直线l于点F,构造特殊Rt△P'FG和Rt△OEF,利用点P坐标和30°、60°的三角函数即可求得P'G的长.
(2)由点B、C、Q的坐标求CQ的长和点C'坐标;过点Q'作x轴的垂线段Q'H,易证△CBQ∽△CHQ',故有![]() ,求得CH、HQ'的长即求得点Q'坐标,进而得到向右向上平移的距离,求得点A'、C'的坐标.求直线CQ解析式,设CQ上的点M横坐标为m,用两点间距离公式可得用m表示A'M和C'M的长.因为△A'MC'是等腰三角形,分三种情况讨论,得到关于m的方程,求解即求得相应的m的值,进而得点M坐标.
,求得CH、HQ'的长即求得点Q'坐标,进而得到向右向上平移的距离,求得点A'、C'的坐标.求直线CQ解析式,设CQ上的点M横坐标为m,用两点间距离公式可得用m表示A'M和C'M的长.因为△A'MC'是等腰三角形,分三种情况讨论,得到关于m的方程,求解即求得相应的m的值,进而得点M坐标.
(1)如图1,过点O作直线l,使直线l经过第二、四象限且与x轴夹角为60°;
过点P作PF⊥x轴于点E,交OA于点D,交直线l于点F;在PF上截取PP'=1;过点N作NG⊥直线l于点G
∵A(3,3),AB⊥x轴于点B
∴直线OA解析式为y=x,OB=AB=3
∵C(1,0)
∴S△AOC![]() OCAB
OCAB![]() 1×3
1×3![]() ,是定值
,是定值
设P(t,﹣t2+4t)(0<t<3)
∴D(t,t)
∴PD=﹣t2+4t﹣t=﹣t2+3t
∴S△OAP=S△OPD+S△APD![]() PDOE
PDOE![]() PDBE
PDBE![]() PDOB
PDOB![]() (t2﹣3t)
(t2﹣3t)
∴t![]() 时,S△OAP最大
时,S△OAP最大
此时,S四边形PACO=S△AOC+S△OAP最大
yP=﹣(![]() )2+3
)2+3![]()
∴P(![]() ,
,![]() )
)
∴P'E=PE﹣PP'![]() 1
1![]() ,即P'(
,即P'(![]() ,
,![]() )
)
∵点M、N在y轴上且MN=1
∴PP'=MN,PP'∥MN
∴四边形MNP'P是平行四边形
∴PM=P'N
∵∠NGO=90°,∠NOG=90°﹣60°=30°
∴Rt△ONG中,NG![]() NO
NO
∴PM+MN![]() NO=P'N+NG+1
NO=P'N+NG+1
∴当点P'、N、G在同一直线上,即P'G⊥直线l时,PM+MN![]() NO=P'G+1最小
NO=P'G+1最小
∵OE![]() ,∠EOF=60°,∠OEF=90°
,∠EOF=60°,∠OEF=90°
∴Rt△OEF中,∠OFE=30°,tan∠EOF![]()
∴EF![]() OE
OE![]()
∴P'F=P'E+EF![]()
∴Rt△P'GF中,P'G![]() P'F
P'F![]()
∴P'G+1![]() 1
1![]()
∴PM+MN![]() NO的最小值为
NO的最小值为![]()
(2)延长A'Q'交x轴于点H
∵C(1,0),Q(3,1),QB⊥x轴于点B
∴CB=2,BQ=1
∴CQ![]()
∵△AQC沿直线AB翻折得△AQC'
∴B(3,0)是CC'的中点
∴C'(5,0)
∵平移距离QQ'=3![]()
∴CQ'=CQ+QQ'=4![]()
∵QB∥Q'H
∴△CBQ∽△CHQ'
∴![]()
∴CH=4CB=8,yQ'=HQ'=4BQ=4
∴xQ'=OC+CH=1+8=9
∴Q'(9,4)
∴点Q(3,1)向右平移6个单位,向上平移3个单位得到点Q'(9,4)
∴A'(9,6),C'(11,3)
∴A'C'![]()
设直线CQ解析式为y=kx+b
∴![]() 解得:
解得:
∴直线CQ:y![]() x
x![]()
设射线CQ上的点M(m,![]() m
m![]() )(m>1)
)(m>1)
∴A'M2=(9﹣m)2+(6![]() m
m![]() )2=(9﹣m)2+(
)2=(9﹣m)2+(![]() m)2
m)2
C'M2=(11﹣m)2+(3![]() m
m![]() )2=(11﹣m)2+(
)2=(11﹣m)2+(![]() m)2
m)2
∵△A'MC'是等腰三角形
①若A'M=A'C',则(9﹣m)2+(![]() m)2=13
m)2=13
解得:m1=7,m2![]()
∴M(7,3)或(![]() ,
,![]() )
)
②若C'M=A'C',则(11﹣m)2+(![]() m)2=13
m)2=13
解得:m1![]() ,m2=13
,m2=13
∴M(![]() ,
,![]() )或(13,6)
)或(13,6)
③若A'M=C'M,则(9﹣m)2+(![]() m)2=(11﹣m)2+(
m)2=(11﹣m)2+(![]() m)2
m)2
解得:m=10
∴M(10,![]() )
)
综上所述,点M坐标为(7,3),(![]() ,
,![]() ),(
),(![]() ,
,![]() ),(13,6),(10,
),(13,6),(10,![]() ).
).



 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】中考将近,同学们需要花更多的时间来进行自我反思和总结,消化白天的学习内容,提高学习效率.因此,每个班都在积极地进行自我调整.我校A班和B班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
A班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)
18 11 22 25 25 18 27 25 22 27
B班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据:
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 23 | 30 | 30 | 59.7 |
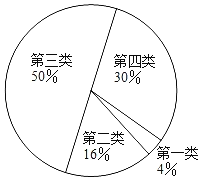
B班的同学还将自主复习时间分为四大类:第一类为时间小于10分钟以下;第二类为时间大于或等于10分钟且小于20分钟;第三类为时间大于或等于20分钟且小于30分钟;第四类为时间大于或等于30分钟,并得到如下的扇形图.
(1)在扇形图中,第一类所对的圆心角度数为 .
(2)写出A班被调查同学的以下特征数.
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 25 | 16 |
(3)从上面的数据,我们可以得到 班的自主复习情况要好一些.其理由为(至少两条): .