题目内容
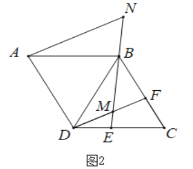
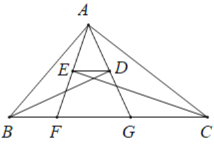
【题目】如图,已知BD⊥AG,CE⊥AF,BD、CE分别是∠ABC和∠ACB的角平分线,若BF=3,ED=2,GC=5,则△ABC的周长为_____.
【答案】28
【解析】
由AG⊥BD,AF⊥CE,BD、CF分别是∠ABC和∠ACB的角平分线推出即△ABG和△ACF都是等腰三角形.根据三角形中位线定理可得FG=2DE=6,然后根据周长公式即可解题.
∵AG⊥BD,BD是∠ABC,BD、CE分别是∠ABC和∠ACB的角平分线,
∴AB=GB,AC=FC,
即△ABG和△ACF都是等腰三角形.
又因AG⊥BD,AF⊥CE,所以E、D为别是AF和AG 的中点,
即ED是△AFG的中位线,
∴FG=2DE=4,
∴AB=BG=3+4=7,AC=CF=5+4=9,
则△ABC的周长为:AB+BC+AC=AB+BF+FG+CG+AC=7+3+4+5+9=28.
故答案为:28.

练习册系列答案
相关题目