��Ŀ����
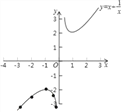
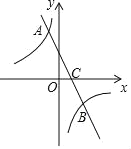
����Ŀ��ij��ѧ��ȤС��Ժ���y=x+![]() ��ͼ������ʽ�����̽����̽���������£��벹��������
��ͼ������ʽ�����̽����̽���������£��벹��������
x | �� | ��3 | ��2 | ��1 | - | - |
|
| 1 | 2 | 3 | �� |
y | �� | - | m | ��2 | - | - |
|
| 2 |
|
| �� |
��1���Ա���x��ȡֵ��Χ���� ����m=�� ����
��2�����ݣ�1���б��ڵ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬��������ͼ���һ���֣����㻭���ú���ͼ�����һ���֣�
��3��������ݺ���ͼ��д�������ú��������ʣ�
��4����һ��̽���ú�����ͼ���֣�
�ٷ���x+![]() =3���� ����ʵ������
=3���� ����ʵ������
��������x�ķ���x+![]() =t��2��ʵ��������t��ȡֵ��Χ���� ����
=t��2��ʵ��������t��ȡֵ��Χ���� ����
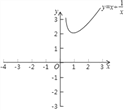
���𰸡���1��x��0����![]() ����2������������3���ٺ���ͼ�����ԭ�����ĶԳƣ��ڵ�x��1ʱ��y��ֵ��xֵ�����������4����2����t����2��t��2��
����2������������3���ٺ���ͼ�����ԭ�����ĶԳƣ��ڵ�x��1ʱ��y��ֵ��xֵ�����������4����2����t����2��t��2��
�������������������1���ɷ�ĸ����Ϊ�㣬���ɵó��Ա���x��ȡֵ��Χ��
��2����㡢���ߣ���������ͼ�ɣ�
��3�����ݺ�����ͼ�õ�д����Ӧ���������ʼ��ɣ�
��4���ٸ�������֪���̵Ľ⣬��Ϊ������ͼ����y=3�Ľ���ĸ�����
�ڸ���ͼ��ĵ�λ�ã��õ����������������t��ȡֵ��Χ.
����������⣺��1����x�ڷ�ĸ�ϣ���x��0��
��x=��2ʱ��m=y=��2+![]() =��
=��![]() ��
��
�ʴ�Ϊ��x��0����![]() ��
��
��2����㡢���ߣ���������ͼ����ͼ��ʾ��
��3���۲캯��ͼ���ҳ��������ʣ�
�ٺ���ͼ�����ԭ�����ĶԳƣ��ڵ�x��1ʱ��y��ֵ��xֵ�����������
��4���ٷ���x+![]() =3�ɿ��ɺ���y=x+
=3�ɿ��ɺ���y=x+![]() ��ͼ����ֱ��y=3�Ľ���ĸ�����
��ͼ����ֱ��y=3�Ľ���ĸ�����
�ߺ���y=x+![]() ��ͼ����ֱ��y=3���������㣬
��ͼ����ֱ��y=3���������㣬
���x+![]() =3��2��ʵ������
=3��2��ʵ������
�ʴ�Ϊ��2��
�ڹ۲캯��ͼ���֪����t����2��t��2ʱ������y=x+![]() ��ͼ����ֱ��y=t���������㣮
��ͼ����ֱ��y=t���������㣮
�ʴ�Ϊ��t����2��t��2��