题目内容
【题目】如图,∠MAN=60°,点B在射线AM上,AB=4,点P为直线AN上一动点,以BP为边作等边三角形BPQ(点B,P,Q按顺时针排列),点O是△BPQ的外心.
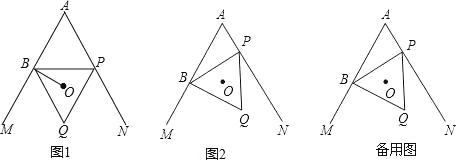
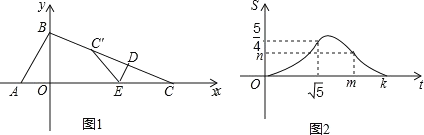
(1)如图1,当OB⊥AM时,点O________∠MAN的平分线上(填“在”或“不在”);
(2)求证:当点P在射线AN上运动时,总有点O在∠MAN的平分线;
(3)当点P在射线AN上运动(点P与点A不重合)时,AO与BP交于点C,设AP=m,用m表示AC·AO;
(4)若点D在射线AN上,AD=2,圆I为△ABD的内切圆.当△BPQ的边BP或BQ与圆I相切时,请直接写出点A与点O的距离.
【答案】(1)在;(2)见解析;(3)4m;(4)OA=2![]() 或OA=
或OA=![]() 或AO=0.
或AO=0.
【解析】
试题分析:(1)在.理由:如图1所示:连接OP.
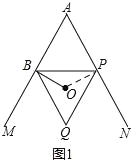
∵点O为等边△BQP的外心,∴∠BOP=2∠BQP=120°,OB=OP.∵OB⊥AM,∴∠ABO=90°.
∵∠A+∠ABO+∠BOP+∠OPA=180°,∴∠OPA=90°.∴OP⊥AN.∵OP=OB,OP⊥AN,OB⊥AM,∴点O在∠MAN的平分线上.
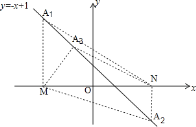
(2)当点A与点P不重合时,如图2所示:连接OB、OP、OA.
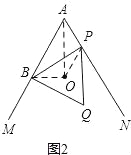
∵点O是等边三角形BOQ的外心,∴∠BOP=120°,OP=OB.∵∠BAP=60°,∴∠BAP+∠BOP=180°.∴点A、B、O、P共圆.又∵OB=OP,∴∠BAO=∠PAO.∴点O在MAN的角平分线上.当点P与点A重合时.∵点O是等边三角形BOQ的外心,∴PO平分∠BPQ.∵∠BPQ与∠MAN重合,∴∠PO平分∠MAN.综上所示,总有点O在∠MAN的平分线.
(3)如图3所示:连接OB、OP、AO.
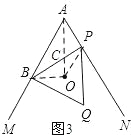
∵由(2)可知点B、O、P、A共圆,∴∠BOA=∠BPA.∵AO平分∠MAN,∴∠BAO=∠PAO.
∴△ABO∽△ACP.∴![]() .∴AC·AO=AB·PA.∴AC·AO=4m.
.∴AC·AO=AB·PA.∴AC·AO=4m.
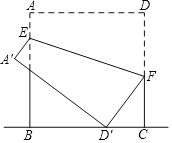
(4)如图4所示:当点P与点D重合时.
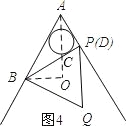
∵∠BAP=60°,BA=4,AD=2,∴BP⊥AP.∴∠BPA=90°.又∵∠PAC=![]() ∠MAN=30°,∴∠OCB=∠ACP=60°.
∠MAN=30°,∴∠OCB=∠ACP=60°.
∵O为等边三角形的外心,∴∠OBC=30°.∴∠BOC=90°.在Rt△AOB中,OA=![]() AB=2
AB=2![]() .
.
如图5所示:当点A与点P重合时.
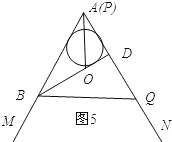
∵∠BAD=60°,BA=4,AD=2,∴BD⊥AQ.∴∠BDA=90°.∵在Rt△AOD中,∠DAO=30°,AD=2,∴AO=AD÷![]() =2×
=2×![]() =
=![]() .
.
如图6所示:
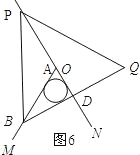
∵∠BAD=60°,BA=4,AD=2,∴BD⊥AN.∴∠BDA=90°.∴∠ABD=30°∵O为△BPQ的外心,∴∠OBD=30°.∴点A与点O重合.∴OA=0.综上所述,OA=2![]() 或OA=
或OA=![]() 或AO=0.
或AO=0.

【题目】中考将近,同学们需要花更多的时间来进行自我反思和总结,消化白天的学习内容,提高学习效率.因此,每个班都在积极地进行自我调整.我校A班和B班的同学也积极响应号召,调查了本班的自习情况以供老师参考.
A班同学在班级抽样调查中,调查了十名同学的学习情况,将这十名同学在一周内每天用于自主复习的总时间四舍五入后,分别记录如下:(单位:分)
18 11 22 25 25 18 27 25 22 27
B班的同学采取的普查方式,让每位同学自己写出平均每天的自主复习时间,将数据收集整理后得到以下数据:
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 23 | 30 | 30 | 59.7 |
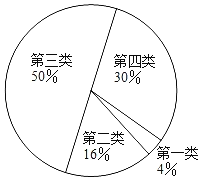
B班的同学还将自主复习时间分为四大类:第一类为时间小于10分钟以下;第二类为时间大于或等于10分钟且小于20分钟;第三类为时间大于或等于20分钟且小于30分钟;第四类为时间大于或等于30分钟,并得到如下的扇形图.
(1)在扇形图中,第一类所对的圆心角度数为 .
(2)写出A班被调查同学的以下特征数.
平均数 | 中位数 | 众数 | 极差 | 方差 |
22 | 25 | 16 |
(3)从上面的数据,我们可以得到 班的自主复习情况要好一些.其理由为(至少两条): .