题目内容
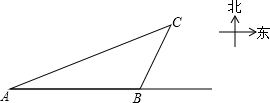
某大草原上有一条笔直的公路,在紧靠公路相距40千米的A,B两地,分别有甲,乙两个医疗站,如图,在A地北偏东45°,B地北偏西60°方向上有一牧民区C.一天,甲医疗队接到牧民区的求救电话,立刻设计了两种救助方案.
方案I:从A地开车沿公路到离牧民区C最近的D处,再开车穿越草地沿DC方向到牧民区C.
方案II:从A地开车穿越草地沿AC方向到牧民区C.已知汽车在公路上行驶的速度是在草地上行驶速度的3倍.
(1)求牧民区到公路的最短距离CD;
(2)你认为甲医疗队设计的两种救助方案,哪一种方案比较合理?并说明理由.(结果精确到0.1,参考数据:
取1.73,
取1.41)

方案I:从A地开车沿公路到离牧民区C最近的D处,再开车穿越草地沿DC方向到牧民区C.
方案II:从A地开车穿越草地沿AC方向到牧民区C.已知汽车在公路上行驶的速度是在草地上行驶速度的3倍.
(1)求牧民区到公路的最短距离CD;
(2)你认为甲医疗队设计的两种救助方案,哪一种方案比较合理?并说明理由.(结果精确到0.1,参考数据:
| 3 |
| 2 |

(1)设CD为x千米,由题意得,∠CBD=30°,∠CAD=45°,
∴AD=CD=x,
在Rt△BCD中,tan30°=
=
,所以BD=
x
∵AD+DB=AB=40,∴x+
x=40
解得x=20
-20≈14.6
所以,牧民区到公路的最短距离CD为14.6千米;
(2)设汽车在草地上行驶的速度为v,则在公路上行驶的速度为3v,
在Rt△ADC中,∠CAD=45°,∴AC=
CD,
方案I用的时间t1=
+
=
=
方案II用的时间t2=
=
(6分)
∴t1-t2=
-
=-
∵3
≈4.2,
∴3
-4>0,
∴t1-t2<0.
所以方案II用的时间多,方案I比较合理.
∴AD=CD=x,
在Rt△BCD中,tan30°=
| ||
| 3 |
| x |
| BD |
| 3 |
∵AD+DB=AB=40,∴x+
| 3 |
解得x=20
| 3 |
所以,牧民区到公路的最短距离CD为14.6千米;
(2)设汽车在草地上行驶的速度为v,则在公路上行驶的速度为3v,
在Rt△ADC中,∠CAD=45°,∴AC=
| 2 |
方案I用的时间t1=
| AD |
| 3v |
| CD |
| v |
| AD+3CD |
| 3v |
| 4CD |
| 3v |
方案II用的时间t2=
| AC |
| v |
| ||
| v |
∴t1-t2=
| 4CD |
| 3V |
| ||
| V |
(3
| ||
| 3v |
∵3
| 2 |
∴3
| 2 |
∴t1-t2<0.
所以方案II用的时间多,方案I比较合理.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目