题目内容
【题目】如图，一次函数y=﹣x+3的图象与反比例y= 
（k为常数，且k≠0）的图象交于A（1，a），B两点．
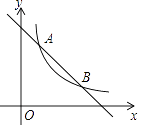
（1）求反比例函数的表达式及点B的坐标；
（2）在x轴上找一点P，使PA+PB的值最小，求满足条件的点P的坐标．
【答案】
（1）
解：∵点A（1，a）在一次函数y=﹣x+3的图象上，
∴a=﹣1+3=2，
∴点A（1，2）．
∵点A（1，2）在反比例y= 
（k为常数，且k≠0）的图象上，
∴k=1×2=2，
∴反比例函数的表达式为y= 
．
联立一次函数与反比例函数关系式成方程组，得：
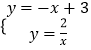，解得： 
， 
，
∴点B（2，1）
（2）
解：作B点关于x轴的对称点B′（2，﹣1），连接AB’，交x轴于点P，连接PB，如图所示．
∵点B、B′关于x轴对称，
∴PB=PB′．
∵点A、P、B′三点共线，
∴此时PA+PB取最小值．
设直线AB′的函数表达式为y=mx+n（m≠0），
将A（1，2）、B（2，﹣1）代入y=mx+n，
，解得： 
，
∴直线AB′的函数表达式为y=﹣3x+5．
当y=﹣3x+5=0时，x= 
，
∴满足条件的点P的坐标为（ ，0）．
【解析】（1）将x=1代入直线AB的函数表达式中即可求出点A的坐标，由点A的坐标利用反比例函数图象上点的坐标特征即可求出反比例函数的表达式，联立两函数表达式成方程组，通过解方程组即可求出点B的坐标；（2）作B点关于x轴的对称点B′（2，﹣1），连接AB’，交x轴于点P，连接PB，由两点之间线段最短可得出此时PA+PB取最小值，根据点A、B′的坐标利用待定系数法可求出直线AB′的函数表达式，再利用一次函数图象上点的坐标特征即可求出点P的坐标．
练习册系列答案
相关题目
