题目内容
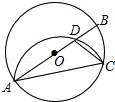
【题目】如图,在平面直角坐标系中,抛物线与x轴交于A、D两点,与y轴交于点B,四边形OBCD是矩形,点A的坐标为(1,0),点D的坐标为(﹣3,0),点B的坐标为(0,4),已知点E(m,0)是线段DO上的动点,过点E作PE⊥x轴交抛物线于点P,交BC于点G,交BD于点H.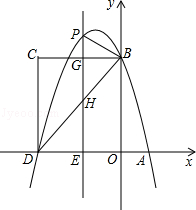
(1)求该抛物线的解析式;
(2)当点P在直线BC上方时,请用含m的代数式表示PG的长度;
(3)在(2)的条件下,是否存在这样的点P,使得以P、B、G为顶点的三角形与△DEH相似?若存在,求出此时m的值;若不存在,请说明理由.
【答案】
(1)
解:设抛物线解析式为y=a(x﹣1)(x+3),
把B(0,4)代入得a(﹣1)3=4,解得a=﹣ ![]() ,
,
所以抛物线解析式为y=﹣ ![]() (x﹣1)(x+3),
(x﹣1)(x+3),
即y=﹣ ![]() x2﹣
x2﹣ ![]() x+4
x+4
(2)
解:当y=4时,﹣ ![]() x2﹣
x2﹣ ![]() x+4=4,解得x1=0,x2=﹣2,
x+4=4,解得x1=0,x2=﹣2,
∴﹣2<m<0,
∵E(m,0),PE⊥x轴,
∴P(m,﹣ ![]() m2﹣
m2﹣ ![]() m+4),
m+4),
而BC∥x轴,
∴G(m,4),
∴PG=﹣ ![]() m2﹣
m2﹣ ![]() m+4﹣4=﹣
m+4﹣4=﹣ ![]() m2﹣
m2﹣ ![]() m(﹣2<m<0)
m(﹣2<m<0)
(3)
解:∵HE∥OB,
∴△DEH∽△DOB,
∵∠PGB=∠DOB,
∴当 ![]() =
= ![]() 时,△PGB∽△BOD,则△PGB∽△HED,
时,△PGB∽△BOD,则△PGB∽△HED,
即 ![]() =
= ![]() ,整理得m2+m=0,解得m1=0(舍去),m2=﹣1,
,整理得m2+m=0,解得m1=0(舍去),m2=﹣1,
当 ![]() =
= ![]() 时,△PGB∽△DOB,则△PGB∽△DEH,
时,△PGB∽△DOB,则△PGB∽△DEH,
即 ![]() =
= ![]() ,整理得16m2+23m=0,解得m1=0(舍去),m2=﹣
,整理得16m2+23m=0,解得m1=0(舍去),m2=﹣ ![]() ,
,
综上所述,在(2)的条件下,存在点P,使得以P、B、G为顶点的三角形与△DEH相似,此时m的值为﹣1或﹣ ![]()
【解析】(1)设交点式y=a(x﹣1)(x+3),然后把B点坐标代入求出a即可得到抛物线解析式;(2)先解方程﹣ ![]() x2﹣
x2﹣ x+4=4,解得x1=0,x2=﹣2,则﹣2<m<0,设P(m,﹣
![]() m2﹣
m2﹣ ![]() m+4),G(m,4),则可用m表示PG;(3)易得△DEH∽△DOB,则判定△PGB与△BOD,由于∠PGB=∠DOB,根据相似三角形的判定方法,当
m+4),G(m,4),则可用m表示PG;(3)易得△DEH∽△DOB,则判定△PGB与△BOD,由于∠PGB=∠DOB,根据相似三角形的判定方法,当 ![]() =
= ![]() 时,△PGB∽△BOD,则△PGB∽△HED,当
时,△PGB∽△BOD,则△PGB∽△HED,当 ![]() =
= ![]() 时,△PGB∽△DOB,则△PGB∽△DEH,然后分别利用相似比列关于m的方程,再解方程求出m,从而得到满足条件的m的值.
时,△PGB∽△DOB,则△PGB∽△DEH,然后分别利用相似比列关于m的方程,再解方程求出m,从而得到满足条件的m的值.

 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案【题目】某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩色页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩色页300元/张,黑白页50元/张;印刷费与印数的关系见表.
印数a (单位:千册) | 1≤a<5 | 5≤a<10 |
彩色 (单位:元/张) | 2.2 | 2.0 |
黑白(单位:元/张) | 0.7 | 0.6 |
(1)直接写出印制这批纪念册的制版费为多少元;
(2)若印制6千册,那么共需多少费用?
(3)如印制x(1≤x<10)千册,所需费用为y元,请写出y与x之间的关系式.