题目内容
【题目】如图,等腰直角△ABC中,AB=AC=8,以AB为直径的半圆O交斜边BC于D,则阴影部分面积为(结果保留π)( ) 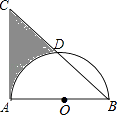
A.16
B.24﹣4π
C.32﹣4π
D.32﹣8π
【答案】B
【解析】解:连接AD,OD, 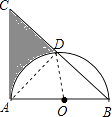
∵等腰直角△ABC中,
∴∠ABD=45°.
∵AB是圆的直径,
∴∠ADB=90°,
∴△ABD也是等腰直角三角形,
∴ ![]() =
= ![]() .
.
∵AB=8,
∴AD=BD=4 ![]() ,
,
∴S阴影=S△ABC﹣S△ABD﹣S弓形AD
=S△ABC﹣S△ABD﹣(S扇形AOD﹣ ![]() S△ABD)
S△ABD)
= ![]() ×8×8﹣
×8×8﹣ ![]() ×4
×4 ![]() ×4
×4 ![]() ﹣
﹣ ![]() +
+ ![]() ×
× ![]() ×4
×4 ![]() ×4
×4 ![]() =16﹣4π+8
=16﹣4π+8
=24﹣4π.
故选B.
连接AD,因为△ABC是等腰直角三角形,故∠ABD=45°,再由AB是圆的直径得出∠ADB=90°,故△ABD也是等腰直角三角形,所以 ![]() =
= ![]() ,S阴影=S△ABC﹣S△ABD﹣S弓形AD由此可得出结论.
,S阴影=S△ABC﹣S△ABD﹣S弓形AD由此可得出结论.

练习册系列答案
相关题目
【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?