题目内容
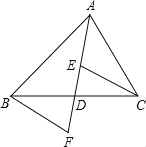
【题目】如图,在△ABC中,点D是BC的中点,连接AD,E,F分别是AD和AD延长线上的点.且DE=DF,连接BF,CE,下列说法中:①△ABD和△ACD的面积相等;②∠BAD=∠CAD;③BF∥CE;④CE=BF,其中,正确的说法有__________(填序号)
【答案】①③
【解析】
根据三角形中线的定义可得BD=CD,根据等底等高的三角形的面积相等判断出①正确,然后利用“边角边”证明△BDF和△CDE全等,根据全等三角形对应边相等可得CE=BF,全等三角形对应角相等可得∠F=∠CED,再根据内错角相等,两直线平行可得BF∥CE.
解:∵AD是△ABC的中线,
∴BD=CD,
∴△ABD和△ACD面积相等,故①正确;
∵AD为△ABC的中线,
∴BD=CD,∠BAD和∠CAD不一定相等,故②错误;
在△BDF和△CDE中,
∵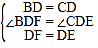 ,
,
∴△BDF≌△CDE(SAS),
∴∠F=∠DEC,
∴BF∥CE,故③正确;
∵△BDF≌△CDE,
∴CE=BF,故④错误,
正确的结论为:①③,
故答案为:①③.

练习册系列答案
相关题目
【题目】一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三方面为选手打分,各项成绩均按百分制,进入决赛的两名选手的单项成绩如下表所示:
选手 | 演讲内容 | 演讲能力 | 演讲效果 |
甲 | 85 | 95 | 95 |
乙 | 95 | 85 | 95 |
(1)如果认为这三方面的成绩同等重要,从他们的成绩看,谁能胜出?
(2)如果按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例计算甲、乙的平均成绩,那么谁将胜出?