题目内容
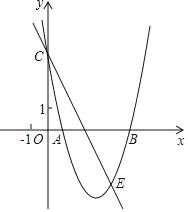
【题目】如图,在平面直角坐标系中,Rt△ABC的三个顶点分别是A(-4, 1),B(-1,3),C(-1,1)
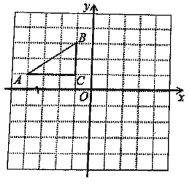
(1)将△ABC以原点O为旋转中心旋转180°,画出旋转后对应的△![]() ;平移△ABC,若A对应的点
;平移△ABC,若A对应的点![]() 坐标为(-4,-5),画出△
坐标为(-4,-5),画出△![]() ;
;
(2)若△![]() 绕某一点旋转可以得到△
绕某一点旋转可以得到△![]() ,直接写出旋转中心坐标是__________;
,直接写出旋转中心坐标是__________;
(3)在x轴上有一点P是的PA+PB的值最小,直接写出点P的坐标___________;
【答案】(1)见解析(2)(-1,-2)(3)P(-![]() ,0).
,0).
【解析】
(1)根据旋转变换与平移变换的定义作出变换后的对应点,再顺次连接即可;
(2)结合对应点的位置,根据旋转变换的性质可得旋转中心;
(3)作出点A关于x轴的对称点A’,再连接A’B,与x轴的交点即为P点.
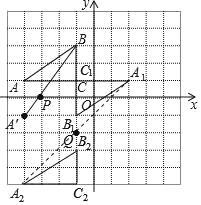
(1)如图所示,△![]() ,△
,△![]() 即为所求;
即为所求;
(2)如图所示,点Q即为所求,坐标为(-1,-2)
(3)如图所示,P即为所求,
设A’B的解析式为y=kx+b,
将A’(-4,-1),B(-1,3)代入得![]()
解得
∴A’B的解析式为y=![]() x+
x+![]() ,
,
当y=0,时,![]() x+
x+![]() =0,解得x=-
=0,解得x=-![]()
∴P(-![]() ,0).
,0).

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目