Question

【题目】如图1，将两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°．若固定△ABC，将△DEC绕点C旋转．

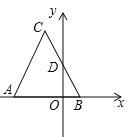
（1）当△DEC统点C旋转到点D恰好落在AB边上时，如图2．

①当∠B=∠E=30°时，此时旋转角的大小为 ；

②当∠B=∠E=α时，此时旋转角的大小为 (用含a的式子表示)．

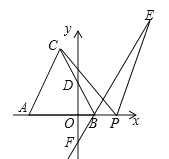
（2）当△DEC绕点C旋转到如图3所示的位置时，小杨同学猜想：△BDC的面积与△AEC的面积相等，试判断小杨同学的猜想是否正确，若正确，请你证明小杨同学的猜想．若不正确，请说明理由．

Answer 1

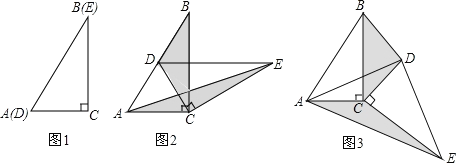
【答案】（1）①60°；②2α；（2）小杨同学猜想是正确的．证明见解析．

【解析】

（1）①证明△ADC是等边三角形即可．
②如图2中，作CH⊥AD于H．想办法证明∠ACD=2∠B即可解决问题．
（2）小扬同学猜想是正确的．过B作BN⊥CD于N，过E作EM⊥AC于M，如图3，想办法证明△CBN≌△CEM（AAS）即可解决问题．

解：（1）①∵∠B=30°，∠ACB=90°，

∴∠CAD=90°﹣30°=60°．

∵CA=CD，

∴△ACD是等边三角形，

∴∠ACD=60°，

∴旋转角为60°．

故答案为：60°．

②如图2中，作CH⊥AD于H．

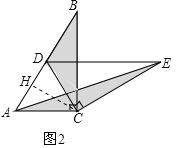
∵CA=CD，CH⊥AD，

∴∠ACH=∠DCH．

∵∠ACH+∠CAB=90°，∠CAB+∠B=90°，

∴∠ACH=∠B，

∴∠ACD=2∠ACH=2∠B=2α，

∴旋转角为2α．

故答案为：2α．

（2）小杨同学猜想是正确的．证明如下：

过B作BN⊥CD于N，过E作EM⊥AC于M，如图3，

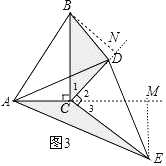
∵∠ACB=∠DCE=90°，

∴∠1+∠2=90°，∠3+∠2=90°，

∴∠1=∠3．

∵BN⊥CD于N，EM⊥AC于M，

∴∠BNC=∠EMC=90°．

∵△ACB≌△DCE，

∴BC=EC，

在△CBN和△CEM中，

∠BNC=∠EMC，∠1=∠3，BC=EC，

∴△CBN≌△CEM(AAS)，

∴BN=EM．

∵S△BDCCDBN，S△ACEACEM．

∵CD=AC，

∴S△BDC=S△ACE．