Question

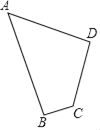
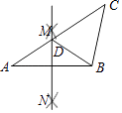
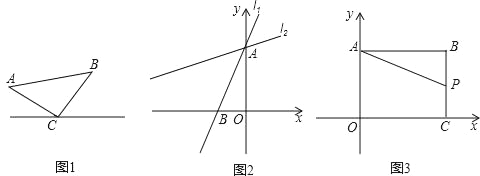
【题目】建立模型：如图1，已知△ABC，AC=BC，∠C=90°，顶点C在直线l上．

实践操作：过点A作AD⊥l于点D，过点B作BE⊥l于点E，求证：△CAD≌△BCE．

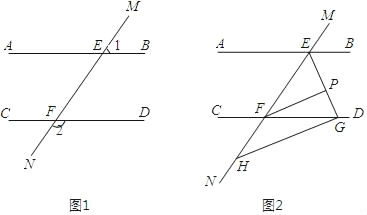
模型应用：（1）如图2，在直角坐标系中，直线l1：y=x+4与y轴交于点A，与x轴交于点B，将直线l1绕着点A顺时针旋转45°得到l2．求l2的函数表达式．

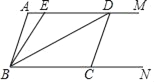
（2）如图3，在直角坐标系中，点B（8，6），作BA⊥y轴于点A，作BC⊥x轴于点C，P是线段BC上的一个动点，点Q（a，2a﹣6）位于第一象限内．问点A、P、Q能否构成以点Q为直角顶点的等腰直角三角形，若能，请求出此时a的值，若不能，请说明理由．

Answer 1

【答案】实践操作：详见解析；模型应用：（1）y=x+4；（2）A、P、Q可以构成以点Q为直角顶点的等腰直角三角形，a的值为或4．

【解析】

操作：根据余角的性质，可得∠ACD＝∠CBE，根据全等三角形的判定，可得答案；

应用（1）根据自变量与函数值的对应关系，可得A、B点坐标，根据全等三角形的判定与性质，可得CD，BD的长，根据待定系数法，可得AC的解析式；

（2）分两种情况讨论：①当Q在直线AP的下方时，②当Q在直线AP的上方时．根据全等三角形的性质，可得关于a的方程，根据解方程，可得答案．

操作：如图1：

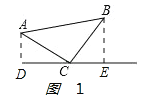
∵∠ACD+∠BCE＝90°，∠BCE+∠CBE＝90°，∴∠ACD＝∠CBE．

在△ACD和△CBE中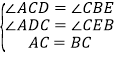，∵，∴△CAD≌△BCE（AAS）；

（1）∵直线yx+4与y轴交于点A，与x轴交于点B，∴A（0，4）、B（﹣3，0）．如图2：

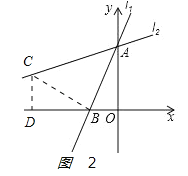
过点B做BC⊥AB交直线l2于点C，过点C作CD⊥x轴．

在△BDC和△AOB中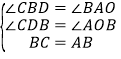，∵，∴△BDC≌△AOB（AAS），∴CD＝BO＝3，BD＝AO＝4．OD＝OB+BD＝3+4＝7，∴C点坐标为（﹣7，3）．

设l2的解析式为y＝kx+b，将A，C点坐标代入，得：，解得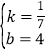：，l2的函数表达式为yx+4；

（2）由题意可知，点Q是直线y＝2x﹣6上一点．分两种情况讨论：

①当Q在直线AP的下方时，如图3，过点Q作EF⊥y轴，分别交y轴和直线BC于点E、F．

在△AQE和△QPF中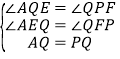，∵，∴△AQE≌△QPF（AAS），AE＝QF，即6﹣（2a﹣6）＝8﹣a，解得：a＝4．

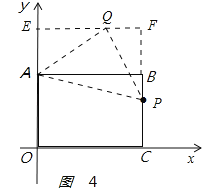
②当Q在直线AP的上方时，如图4，过点Q作EF⊥y轴，分别交y轴和直线BC于点E、F，AE＝2a﹣12，FQ＝8﹣a．

在△AQE和△QPF中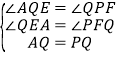，∵，∴△AQE≌△QPF（AAS），AE＝QF，即2a﹣12＝8﹣a，解得：a．

综上所述：A．P、Q可以构成以点Q为直角顶点的等腰直角三角形，a的值为或4．