题目内容
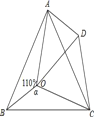
【题目】如图,⊙O是△ABC的外接圆,AB为直径,∠BAC的平行线交⊙O与点D,过点D的切线分别交AB、AC的延长线与点E、F.

(1)求证:AF⊥EF.
(2)小强同学通过探究发现:AF+CF=AB,请你帮忙小强同学证明这一结论.
【答案】(1)首先连接OD,由EF是⊙O的切线,可得OD⊥EF,由∠BAC的平行线交⊙O与点D,易证得OD⊥BC,即可得BC∥EF,由AB为直径,根据直径所对的圆周角是直角,可得AC⊥BC,继而证得AF⊥EF。
(2)首先连接BD并延长,交AF的延长线于点H,连接CD,易证得△ADH≌△ADB,△CDF≌△HDF,继而证得AF+CF=AB。
【解析】
(1)首先连接OD,由EF是⊙O的切线,可得OD⊥EF,由∠BAC的平行线交⊙O与点D,易证得OD⊥BC,即可得BC∥EF,由AB为直径,根据直径所对的圆周角是直角,可得AC⊥BC,继而证得AF⊥EF。
(2)首先连接BD并延长,交AF的延长线于点H,连接CD,易证得△ADH≌△ADB,△CDF≌△HDF,继而证得AF+CF=AB。
证明:(1)连接OD,

∵EF是⊙O的切线,∴OD⊥EF。
∵AD平分∠BAC,∴∠CAD=∠BAD。
∴![]() 。∴OD⊥BC。∴BC∥EF。
。∴OD⊥BC。∴BC∥EF。
∵AB为直径,∴∠ACB=90°,即AC⊥BC。
∴AF⊥EF。
(2)连接BD并延长,交AF的延长线于点H,连接CD,

∵AB是直径,∴∠ADB=90°,即AD⊥BH。
∴∠ADB=∠ADH=90°,
∵在△ABD和△AHD中, ,
,
∴△ABD≌△AHD(ASA)。∴AH=AB。
∵EF是切线,∴∠CDF=∠CAD,∠HDF=∠EDB=∠BAD。∴∠EDF=∠HDF。
∵DF⊥AF,DF是公共边,∴△CDF≌△HDF(ASA)。∴FH=CF。
∴AF+CF=AF+FH=AH=AB,即AF+CF=AB。

 阅读快车系列答案
阅读快车系列答案