��Ŀ����
����Ŀ���龳�۲죺
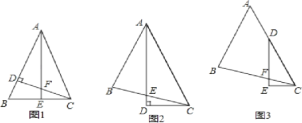
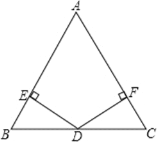
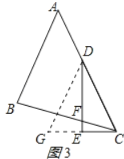
��ͼ1����ABC�У�AB=AC����BAC=45����CD��AB��AE��BC������ֱ�ΪD��E��CD��AE���ڵ�F��
��д��ͼ1�����е�ȫ�������� ��
���߶�AF���߶�CE��������ϵ�� ��
����̽����
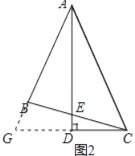
��ͼ2����ABC�У���BAC=45����AB=BC��ADƽ�֡�BAC��AD��CD������ΪD��AD��BC���ڵ�E��
��֤��AE=2CD��
��չ���죺
��ͼ3����ABC�У���BAC=45����AB=BC����D��AC�ϣ���EDC=![]() ��BAC��DE��CE������ΪE��DE��BC���ڵ�F����֤��DF=2CE��
��BAC��DE��CE������ΪE��DE��BC���ڵ�F����֤��DF=2CE��
Ҫ������д�������ߵ�����������ͼ3�л��������ߣ�����Ҫ֤����
���𰸡�1���١�ABE�ա�ACE����ADF�ա�CDB����AF=2CE����������2.��������3.������
��������
�龳�۲죺����ȫ�������ε��ж��������ó������
����ȫ�������ε����ʼ��ɵó����ۣ�
����̽�����ӳ�AB��CD���ڵ�G����ASA֤����ADC�ա�ADG���ó���Ӧ�����CD=GD����CG=2CD��֤����BAE=��BCG����ASA֤����ADC�ա�CBG���ó�AE=CG=2CD���ɣ�
��չ���죺��DG��BC��CE���ӳ�����G��ͬ��֤��������ȫ�ȣ��ó�DF=CG���ɣ�
��ͼ1�����е�ȫ��������Ϊ��ABE�ա�ACE����ADF�ա�CDB���ʴ�Ϊ����ABE�ա�ACE����ADF�ա�CDB
���߶�AF���߶�CE��������ϵ�ǣ�AF=2CE���ʴ�Ϊ��AF=2CE��
����̽����
֤�����ӳ�AB��CD���ڵ�G����ͼ2��ʾ��
��ADƽ�֡�BAC��
���CAD=��GAD��
��AD��CD��
���ADC=��ADG=90����
����ADC����ADG��
![]()
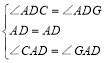 ��
��
���ADC�ա�ADG��ASA����
��CD=GD����CG=2CD��
�ߡ�BAC=45����AB=BC��
���ABC=90����
���CBG=90����
���G+��BCG=90����
�ߡ�G+��BAE=90����
���BAE=��BCG��
����ABE����CBG��
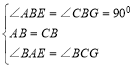 ��
��
���ADC�ա�CBG�У�ASA����
��AE=CG=2CD��
��չ���죺
�⣺��DG��BC��CE���ӳ�����G��
��ͼ3��ʾ��

����Ŀ�����������з���Ͷ�ţ�����Ч��߶������Ĵ����������ã�������Ⱦ����������.Ϊ���˽�ͬѧ�Ƕ���������֪ʶ���˽�̶ȣ���ǿͬѧ�ǵĻ�����ʶ���ռ��������༰Ͷ�ŵ����֪ʶ��ijУ��ѧ��ȤС���ͬѧ�����������������֪ʶ��Ͷ��������ʾ������ڱ�У�����ȡ������ͬѧ�������ʾ����ԣ����ݲ��Գɼ��ֲ���������ǽ�ȫ�����Գɼ��ֳ�![]() ��
��![]() ��
��![]() ��
��![]() ���飬����������ͳ��ͼ����
���飬����������ͳ��ͼ����
����������֪ʶ��Ͷ��������ʾ����Գɼ�ͳ��ͼ��
��� | ����/�� | Ƶ�� | �����ܷ�/�� |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
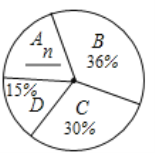
��������ͳ����Ϣ������������⣺
��1�����![]() _____��
_____��![]() ______��
______��
��2����β��Գɼ�����λ������______�飻
��3����ȫ�����Գɼ���ƽ������