题目内容
【题目】已知:如图,抛物线y=ax2+bx+c经过A(1,0)、B(5,0)、C(0,5)三点.
(1)求抛物线的函数关系式;
(2)求抛物线的顶点坐标、对称轴;
(3)若过点C的直线与抛物线相交于点E(4,m),请连接CB,BE并求出△CBE的面积S的值.
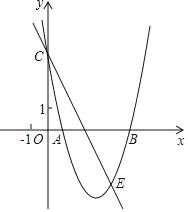
【答案】(1)y=x2﹣6x+5;(2)当x≥3时y随x的增大而增大;(3)10.
【解析】
(1)设抛物线![]() 把C的坐标代入求出即可;
把C的坐标代入求出即可;
(2)把抛物线的解析式化成顶点式,求得对称轴,根据抛物线的性质即可求得x的取值;
(3)求出E的坐标,把C(0,5),E(4,-3)代入y=kx+b得到方程组,求出方程组的解即可得到一次函数的解析式,求出直线与X轴的交点,根据三角形的面积公式求出即可.
(1)∵A(1,0),B(5,0),
设抛物线![]()
把C(0,5)代入得:![]()
解得:a=1,
![]()
即抛物线的函数关系式是![]()
(2)![]()
∴抛物线的对称轴为x=3,
又∵二次函数![]() 的二次项系数为1>0,
的二次项系数为1>0,
∴抛物线的开口向上,
∴当x≥3时y随x的增大而增大;
(3)把x=4代入![]() 得:y=﹣3,
得:y=﹣3,
∴E(4,﹣3),
把C(0,5),E(4,﹣3)代入![]() 得:
得:![]() ,
,
解得:![]()
![]()
设直线![]() 交x轴于D,
交x轴于D,
当y=0时,![]() ,
,
∴x=![]() ,
,
∴OD=![]() ,
,
BD=5﹣![]() =
=![]() ,
,
![]()

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目