题目内容
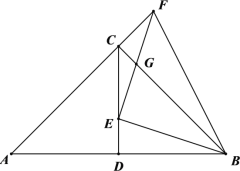
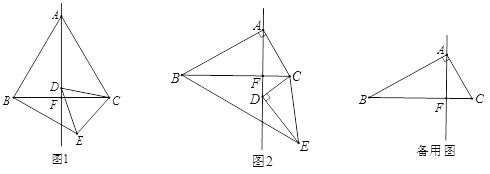
【题目】如图,在等边![]() 和等边
和等边![]() 中,过
中,过![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() .
.
(1)如图,求证:四边形![]() 为菱形;
为菱形;
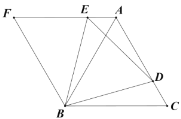
(2)如图,过![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,不添加任何辅助线,直接写出与
,不添加任何辅助线,直接写出与![]() 相等的所有角(不包括
相等的所有角(不包括![]() ).
).
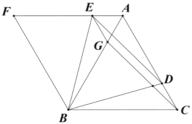
【答案】(1)见详解;(2)与![]() 相等的角有∠ABE,∠CBD,∠ACG,∠DEG.
相等的角有∠ABE,∠CBD,∠ACG,∠DEG.
【解析】
(1)由等边三角形的性质,得到AB=BC=AC,BE=BD,∠ABC=∠BAC=∠EBD=60°,先证明△ABE≌△CBD,则∠BEF=∠BDA,然后证明△FEB≌△ADB,则BF=BA=AC,则四边形AFBC是平行四边形,由BC=AC,即可得到答案;
(2)由三角形的内角和定理,得到∠ABE=∠ADE,由等量代换,得到∠CBD=∠ABE=∠ADE,由平行线的性质得∠ACG=∠ADE,由ASA证明△ABE≌△ACG,则CG=BE=DE,得到四边形CDEG是平行四边形,则∠DEG=∠ACG=∠ADE,即可得到答案.
解:(1)如图:
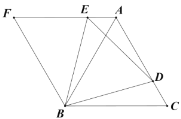
在等边![]() 和等边
和等边![]() 中,
中,
∴AB=BC=AC,BE=BD,∠ABC=∠BAC=∠EBD=60°,
∴∠ABE+∠ABD=∠ABD+∠CBD=60°,
∴∠ABE=∠CBD,
∴△ABE≌△CBD(SAS),
∴∠AEB=∠CDB,
∴∠BEF=∠BDA,
∵BF∥AC,
∴∠ABF=∠BAC=60°,
∵∠FBE+∠ABE=∠ABE+ABD=60°,
∴∠FBE=∠ABD,
∵BE=BD,
∴△FEB≌△ADB,
∴BF=BA=AC,
∴四边形AFBC是平行四边形,
∵BC=AC,
∴四边形AFBC是菱形;
(2)如图:
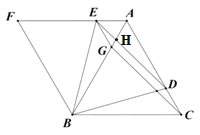
∵∠BED=∠BAC=60°,∠BHE=∠DHA,
∴∠ABE=∠ADE;
由(1)知,∠CBD=∠ABE,
∴∠CBD=∠ADE;
∵CG∥DE,
∴∠ACG=∠ADE;
∴∠ACG=∠ABE,
∵AF∥BC,
∴∠BAE=∠ABC=∠BAC=60°,
∵AB=AC,
∴△ABE≌△ACG,
∴CG=BE=DE,
∵CG∥DE,
∴四边形CDEG是平行四边形,
∴∠DEG=∠ACG=∠ADE;
∴与![]() 相等的角有:∠ABE,∠CBD,∠ACG,∠DEG.
相等的角有:∠ABE,∠CBD,∠ACG,∠DEG.