题目内容
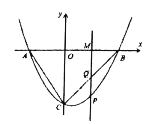
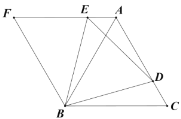
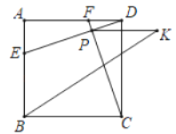
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() ,
,![]() 分别是边
分别是边![]() ,
,![]() 上的动点,
上的动点,![]() ,连接
,连接![]() ,
,![]() 交于点
交于点![]() ,过点
,过点![]() 作
作![]() ,且
,且![]() ,若
,若![]() 的度数最大时,则
的度数最大时,则![]() 长为( )
长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】A
【解析】
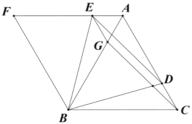
根据全等三角形的性质得到∠ADE=∠DCF,求得∠CPD=90°,得到点P在以CD为直径的半圆上运动,取CD的中点O,过O作OM⊥CD,且点M在CD的右侧,MO=2,连接OP,KM,推出四边形POMK是菱形,于是得到点K在以M为圆心,半径为2的半圆上运动,当BK与⊙M相切时,∠CBK最大,根据勾股定理即可得到结论.
∵正方形ABCD中,AD=CD,∠A=∠CDA=90°,
∵AE=DF,
∴△ADE≌△DCF(SAS),
∴∠ADE=∠DCF,
∵∠ADE+∠CDE=90°,
∴∠DCF+∠CDE=90°,
∴∠CPD=90°,
∴点P在以CD为直径的半圆上运动,
取CD的中点O,过O作OM⊥CD,且点M在CD的右侧,MO=2,
连接OP,KM,过M作MN⊥BC,与BC的延长线交于点N,
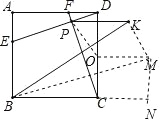
∵PK∥BC,BC⊥CD,
∴PK⊥CD,
∴PK∥OM,PK=OM=2,
∴四边形POMK是平行四边形,
∵CD=AB=4,
∴OP=![]() CD=2,
CD=2,
∴OP=OM,
∴四边形POMK是菱形,
∴点K在以M为圆心,半径为2的半圆上运动,
当BK与⊙M相切时,∠CBK最大,
∴∠BKM=90°,
∵![]() ,
,
∴![]() ,
,
故选:A.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
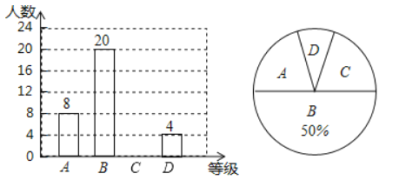
名题训练系列答案【题目】某校为了调查学生对卫生健康知识,特别是疫情防控下的卫生常识的了解,现从九年级![]() 名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
名学生中随机抽取了部分学生参加测试,并根据测试成绩绘制了如下频数分布表和扇形统计图(尚不完整).
组别 | 成绩 | 人数 |
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
第 |
|
|
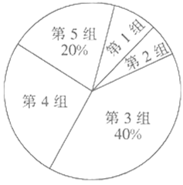
请结合图表信息完成下列各题.
(1)表中a的值为_____,b的值为______;在扇形统计图中,第![]() 组所在扇形的圆心角度数为______°;
组所在扇形的圆心角度数为______°;
(2)若测试成绩不低于![]() 分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
分为优秀,请你估计从该校九年级学生中随机抽查一个学生,成绩为优秀的概率.
(3)若测试成绩在![]() 分以上(含
分以上(含![]() 分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.
分)均为合格,其他为不合格,请你估计该校九年级学生中成绩不合格的有多少人.