题目内容
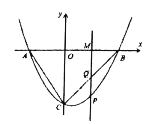
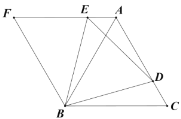
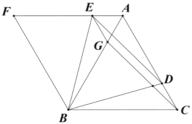
【题目】如图,在矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别在边
分别在边![]() 和
和![]() 上,沿
上,沿![]() 折叠四边形
折叠四边形![]() ,使点
,使点![]() 、
、![]() 分别落在
分别落在![]() 、
、![]() 处,得四边形
处,得四边形![]() ,点
,点![]() 在
在![]() 上,过点
上,过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;
;
③![]() ;④若点
;④若点![]() 是
是![]() 的中点,则
的中点,则![]() ,其中,正确结论的序号是_______.(把所有正确结论的序号都在填在横线上)
,其中,正确结论的序号是_______.(把所有正确结论的序号都在填在横线上)

【答案】①②③
【解析】
由折叠可知∠MNB1=∠BNM,MN⊥BB1,再根据同角的余角相等的性质和等量关系即可判定①正确;根据AA可证△MEN∽△BCB1,可判定②正确;根据相似三角形的性质和等量关系可得![]() ,为定值,可判定③正确;根据相似三角形的性质和勾股定理可得AM=BE=BN-NE=
,为定值,可判定③正确;根据相似三角形的性质和勾股定理可得AM=BE=BN-NE=![]() ,可判定④不正确;从而求解.
,可判定④不正确;从而求解.
解:由折叠可知∠MNB1=∠BNM,MN⊥BB1,
∴∠BNM+∠B1BN=90°,
∵∠ABB1+∠B1BN=90°,
∴∠BNM=∠ABB1,
∴∠MNB1=∠ABB1,故①正确;
∵ME⊥BC,
∴∠MNE+∠NME=90°,
由折叠的性质可得MN⊥BB1,
∴∠MNE+∠B1BN=90°,
∴∠NME=∠BB1N,
∴△MEN∽△BCB1,
故②正确;
由②可知![]() ,
,
∵ME=AB=2,BC=4,
∴![]() ,为定值,故③正确;
,为定值,故③正确;
∵△MEN∽△BCB1,
∴![]() ,
,
∴NE=![]() B1C,
B1C,
∵点![]() 是
是![]() 的中点,
的中点,
∴B1C=![]() DC,
DC,
则NE=![]() DC=
DC=![]() ×2=
×2=![]() ,
,
设BN=x,则NC=4-x,B1N=x,
在Rt△B1NC中,由勾股定理可得x2=(4-x)2+12,
解得x=![]() ,
,
∴AM=BE=BN-NE=![]() ,故④不正确.
,故④不正确.
故答案为:①②③.

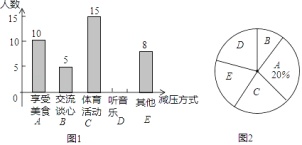
【题目】某校组织全校学生进行了一次“社会主义核心价值观”知识竞赛,赛后随机抽取了各年级部分学生成绩进行统计,制作如下频数分布表和频数分布直方图.请根据图表中提供的信息,解答下列问题:
分数段( | 频数 | 频率 |
| 4 | 0.1 |
| 8 |
|
|
| 0.3 |
| 10 | 0.25 |
| 6 | 0.15 |
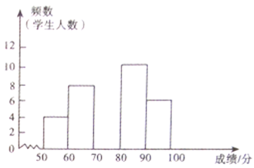
(1)请求出该校随机抽取了____学生成绩进行统计;
(2)表中![]() ____,
____,![]() ____,并补全直方图;
____,并补全直方图;
(3)若用扇形统计图描述此成绩统计分布情况,则分数段![]() 对应扇形的圆心角度数是___
对应扇形的圆心角度数是___![]() ;
;
(4)若该校共有学生8000人,请估计该校分数在![]() 的学生有多少人?
的学生有多少人?