��Ŀ����
����Ŀ��ƽ��ֱ������ϵ�ڴ����ͼ���֮�������һ��������ʵ���˼��η�������������Ľ�ϣ�ʹ������ͳһ����������ƽ��ֱ������ϵ�У���֪��A��x1��y1����B��x2��y2������A��B����֮��ľ�����Ա�ʾΪAB��![]() ������A��2��1����B����1��2������A��B����֮��ľ���AB��
������A��2��1����B����1��2������A��B����֮��ľ���AB��![]() ��
��![]() ����֮������ʽ
����֮������ʽ![]() Ҳ���Կ���ƽ��ֱ������ϵ�еĵ�C��5��1�����D��1����2��֮��ľ��룮
Ҳ���Կ���ƽ��ֱ������ϵ�еĵ�C��5��1�����D��1����2��֮��ľ��룮
��1����֪��M����7��6����N��1��0������M��N�����ľ���Ϊ�� ����
��2�������ʽ![]() ����Сֵ��
����Сֵ��
��3�������ʽ|![]() | ȡ���ֵʱ��x��ȡֵ��
| ȡ���ֵʱ��x��ȡֵ��
���𰸡���1��10����2��13����3��![]()
��������
��1�����������ľ��빫ʽ���ɵõ����ۣ�
��2���ɣ�1����֪��![]() ��ʾx���ϵ�P��x��0�����E��-1��7���ľ���PE�͵�A��x��0�����F��4��5���ľ���PF֮�ͣ�����PE+PF����E����x��ԳƵ�
��ʾx���ϵ�P��x��0�����E��-1��7���ľ���PE�͵�A��x��0�����F��4��5���ľ���PF֮�ͣ�����PE+PF����E����x��ԳƵ�![]() ��-1��-7������Сֵ����
��-1��-7������Сֵ����![]() �����ɣ�1�����ɵõ����ۣ�
�����ɣ�1�����ɵõ����ۣ�
��3��������֪�����õ�![]() ���ɣ�1����֪��|
���ɣ�1����֪��|
��ʾ��A��x��0�����E��2��3���ľ���͵�A��x��0�����F��-![]() ��2���ľ���֮������ֵʱ����ֱ��EF��x��Ľ���ΪA��x��0�������ǵõ����ۣ�
��2���ľ���֮������ֵʱ����ֱ��EF��x��Ľ���ΪA��x��0�������ǵõ����ۣ�
�⣺��1���ߵ�M��-7��6����N��1��0����
��MN=![]() =10��
=10��
��M��N�����ľ�����10��
�ʴ�Ϊ��10��
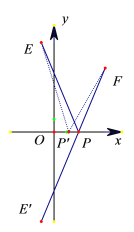
��2���ɣ�1����֪��![]() ��ʾ��P��x��0�����E��-1��7���ľ���͵�A��x��0�����F��4��5���ľ���֮�ͣ�
��ʾ��P��x��0�����E��-1��7���ľ���͵�A��x��0�����F��4��5���ľ���֮�ͣ�
����x���ҵ�һ�㵽EF�ĺ���С���ɽ�������ģ�Ϳ�֪���ԳƵ㣬��E����x��ԳƵ�![]() ��-1��-7��������
��-1��-7��������![]() ����AF+AE=
����AF+AE=![]() Ϊ��Сֵ��
Ϊ��Сֵ��
��![]() ��СֵΪ
��СֵΪ![]() �ij���
�ij���
��EF=![]() =13��
=13��
�����ʽ![]() ����Сֵ��13��
����Сֵ��13��
�ʴ�Ϊ13.
��3����![]() =
=![]() ��
��
���ɣ�1����֪��![]() ��ʾ��P��x��0�����E��2��3���ľ���PE�͵�P��x��0�����F��-
��ʾ��P��x��0�����E��2��3���ľ���PE�͵�P��x��0�����F��-![]() ��2���ľ���֮PF���|PE-PF|��P��E��F���㹲��ʱȡ���ֵʱ����ֱ��EF��x��Ľ���ΪA��x��0����
��2���ľ���֮PF���|PE-PF|��P��E��F���㹲��ʱȡ���ֵʱ����ֱ��EF��x��Ľ���ΪA��x��0����
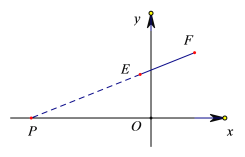
��ֱ��EF�Ľ���ʽΪy=kx+b��
��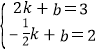 ��
��
��ã�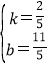 ��
��
��ֱ��EF�Ľ���ʽΪ![]()
��y=0ʱ��x=![]() ��
��
�����ʽ![]() ȡ���ֵʱ��x��ȡֵΪ
ȡ���ֵʱ��x��ȡֵΪ![]() ��
��