题目内容
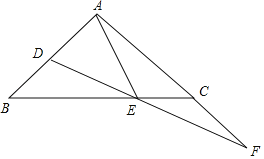
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D,E分别在AB,BC上,∠EAD=∠EDA,点F为DE的延长线与AC的延长线的交点.
(1)求证:DE=EF;
(2)判断BD和CF的数量关系,并说明理由;
(3)若AB=3,AE=![]() ,求BD的长.
,求BD的长.
【答案】(1)证明见解析;(2证明见解析;(3)BD=1.
【解析】
(1)先根据等角对等边得出EA=ED,再在Rt△ADF中根据直角三角形的两锐角互余和等角的余角相等得出∠EAC=∠F,得出EA=EF,等量代换即可解决问题;
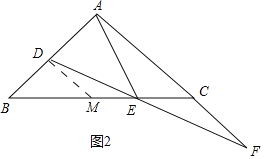
(2)结论:BD=CF.如图2中,在BE上取一点M,使得ME=CE,连接DM.想办法证明DM=CF,DM=BD即可;
(3)如图3中,过点E作EN⊥AD交AD于点N.设BD=x,则DN=![]() ,DE=AE=
,DE=AE=![]() ,由∠B=45°,EN⊥BN.推出EN=BN=x+
,由∠B=45°,EN⊥BN.推出EN=BN=x+![]() =
=![]() ,在Rt△DEN中,根据DN2+NE2=DE2,构建方程即可解决问题.
,在Rt△DEN中,根据DN2+NE2=DE2,构建方程即可解决问题.
(1)证明:如图1中,

![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
(2)解:结论:![]() .
.
理由:如图2中,在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,连接
,连接![]() .
.
![]() .
.![]() ,
,![]() .
.
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
(3)如图3中,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .
.

![]() ,
,![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() .
.
![]() ,
,
在![]() 中,
中,![]() ,
,
![]()
解得![]() 或
或![]() (舍弃)
(舍弃)
![]() .
.

 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】某超市对![]() ,
,![]() 两种商品开展春节促销活动,活动方案有如下两种:
两种商品开展春节促销活动,活动方案有如下两种:
商品 |
|
| |
标价(单位:元) | 120 | 150 | |
方案一 | 每件商品出售价格 | 按标价打7折 | 按标价打 |
方案二 | 若所购商品超过10件(不同商品可累计)时,每件商品均按标价打8折后出售. | ||
(同一种商品不可同时参与两种活动)
(1)某单位购买![]() 商品5件,
商品5件,![]() 商品4件,共花费960元,求
商品4件,共花费960元,求![]() 的值;
的值;
(2)在(1)的条件下,若某单位购买![]() 商品
商品![]() 件(
件(![]() 为正整数),购买
为正整数),购买![]() 商品的件数比
商品的件数比![]() 商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.
商品件数的2倍还多一件,请问该单位该如何选择才能获得最大优惠?请说明理由.
【题目】为弘扬中华民族传统文化,某校举办了“燕城诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 | 分数 | 人数 |
第1组 |
| 16 |
第2组 |
|
|
第3组 |
| 20 |
第4组 |
|
|
第5组 |
| 6 |
请根据以上信息,解答下列问题:
(1)此次随机抽取的学生数是 人,![]() ,
,![]() ;
;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1500名学生,那么成绩低于70分的约有多少人?

【题目】银川九中要举办“不忘初心跟党走”2018年元旦合唱比赛,为迎接比赛,某校区七年级(3)(4)班决定订购同一套服装,两班一共有103人(三班人数多于四班),经协商,某服装店给出的价格如下:
购买人数/人 | 1~50人 | 50~100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么三、四班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
(3)该服装店此次出售的服装每套成本是32元,如果按上面的第(2)问形式购买,请计算这个服装店此次出售服装的利润率是多少?

