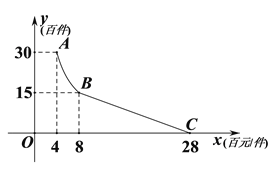
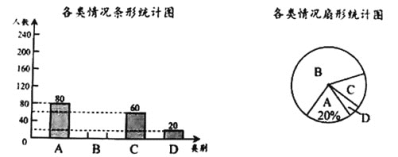
题目内容
【题目】如图,ΔABC中,AB=AC,点E,F在边BC上,BE=CF,点D在AF的延长线上,AD=AC.
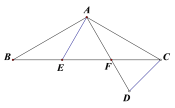
(1)求证:ΔABE≌ΔACF;
(2)若∠BAE=30°,则∠ADC= (直接写答案)
【答案】(1)证明见解析;(2)75°.
【解析】
(1)要证明△ABE≌△ACF,由题意可得AB=AC,∠B=∠ACF,BE=CF,从而可以证明结论成立;
(2)根据(1)中的结论和等腰三角形的性质可以求得∠ADC的度数.
(1)证明:∵AB=AC,
∴∠B=∠ACF,
在△ABE和△ACF中,
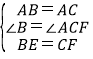 ,,
,,
∴△ABE≌△ACF(SAS);
(2)∵△ABE≌△ACF,∠BAE=30°,
∴∠BAE=∠CAF=30°,
∵AD=AC,
∴∠ADC=∠ACD,
∴∠ADC=![]() =75°,
=75°,
故答案为:75°.

练习册系列答案
相关题目