题目内容
【题目】一个不透明袋子中有1个红球和n个白球，这些球除颜色外无其他差别．
（1）从袋中随机摸出一个球，记录其颜色，然后放回．大量重复该实验，发现摸到红球的频率稳定于0.25，求n的值．
（2）在（1）的条件下，从袋中随机摸出两个球，求两个球颜色不同的概率．
【答案】(1)3;(2)图形见解析，
.
【解析】
（1）利用频率估计概率，则摸到红球的概率为0.25，根据概率公式得到
=0.25，然后解方程即可；
（2）先画树状图展示所有12种等可能的结果数，再找出两次摸出的球颜色不同的结果数，然后根据概率公式求解．
解：（1）利用频率估计概率得到摸到红球的概率为0.25，
则=0.25，
解得n=3；
（2）画树状图为：
共有12种等可能的结果数，其中两次摸出的球的颜色不同的结果共有6种，
所以两次摸出的球颜色不同的概率=
=．
练习册系列答案
相关题目
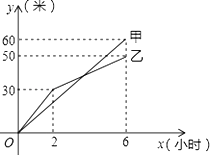
【题目】为了创建“全国文明城市”，鄂州市积极主动建设美丽家园，某社区拟将一块面积为1000m2的空地进行绿化，一部分种草，剩余部分栽花，设种草面积为x（m2），种草费用y1（元）与x（m2）的函数关系式为y1=
，其图象如图所示：栽花所需费用y2（元）与x（m2）的函数关系如表所示：
x（m2） | 100 | 200 | 300 |
y2（元） | 3900 | 7600 | 11100 |
（1）请直接写出y1与种草面积x（m2）的函数关系式，y2与栽花面积x（m2）的函数关系式；
（2）设这块1000m2空地的绿化总费用为W（元），请利用W与种草面积x（m2）的函数关系式，求出绿化总费用W的最大值；
（3）若种草部分的面积不少于600m2，栽花部分的面积不少于200m2，请求出绿化总费用W的最小值．
