题目内容
【题目】问题发现:
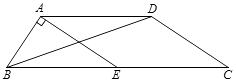
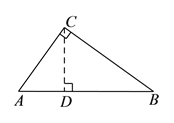
(![]() )如图①,
)如图①,![]() 中,
中,![]() ,
,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上任意一点,则
边上任意一点,则![]() 的最小值为__________.
的最小值为__________.
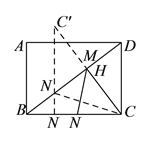
(![]() )如图②,矩形
)如图②,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、点
、点![]() 分别在
分别在![]() 、
、![]() 上,求
上,求![]() 的最小值.
的最小值.
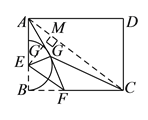
(![]() )如图③,矩形
)如图③,矩形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 边上一点,且
边上一点,且![]() ,点
,点![]() 是
是![]() 边上的任意一点,把
边上的任意一点,把![]() 沿
沿![]() 翻折,点
翻折,点![]() 的对应点为点
的对应点为点![]() ,连接
,连接![]() 、
、![]() ,四边形
,四边形![]() 的面积是否存在最小值,若存在,求这个最小值及此时
的面积是否存在最小值,若存在,求这个最小值及此时![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.



【答案】(1) ![]() ;(2)
;(2) ![]() 的最小值为
的最小值为![]() .(3)
.(3) ![]()
【解析】试题分析:(1)根据两种不同方法求面积公式求解;(2)作![]() 关于
关于![]() 的对称点
的对称点![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,求
,求![]() 的长即可;(3) 连接
的长即可;(3) 连接![]() ,则
,则![]() ,
,![]() ,则点
,则点![]() 的轨迹为以
的轨迹为以![]() 为圆心,
为圆心,![]() 为半径的一段弧.过
为半径的一段弧.过![]() 作
作![]() 的垂线,与⊙
的垂线,与⊙![]() 交于点
交于点![]() ,垂足为
,垂足为![]() ,由
,由![]() 求得GM的值,再由
求得GM的值,再由![]() 求解即可.
求解即可.
试题解析:
(![]() )从
)从![]() 到
到![]() 距离最小即为过
距离最小即为过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,
,
![]() ,
,
∴![]() ,
,
(![]() )作
)作![]() 关于
关于![]() 的对称点
的对称点![]() ,过
,过![]() 作
作![]() 的垂线,垂足为
的垂线,垂足为![]() ,且与
,且与![]() 交于
交于![]() ,
,
则![]() 的最小值为
的最小值为![]() 的长,
的长,
设![]() 与
与![]() 交于
交于![]() ,则
,则![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() 的最小值为
的最小值为![]() .
.
(![]() )连接
)连接![]() ,则
,则![]() ,
,
![]() ,
,
∴点![]() 的轨迹为以
的轨迹为以![]() 为圆心,
为圆心,![]() 为半径的一段弧.
为半径的一段弧.
过![]() 作
作![]() 的垂线,与⊙
的垂线,与⊙![]() 交于点
交于点![]() ,垂足为
,垂足为![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]() .
.

练习册系列答案
相关题目