��Ŀ����
����Ŀ���������ѧϰ��ȫ�������ε��ж���������SSS����SAS����ASA��)�����Ǽ������������������������ߺ�����һ�ߵĶԽǶ�Ӧ����������ν����о�.
����˼�����������÷������Ա�ʾΪ������ABC����DEF�У�AC=DF��BC=EF����ABC=��DEF.Ȼ��ԡ�ABC���з��࣬�ɷ�Ϊ����ABC����ǡ�ֱ�ǡ��۽��������������̽����
��һ�����������ABC�����ʱ��AB=DE��һ��������
�ڶ������������ABC��ֱ��ʱ��������HL�����ɵ���ABC����DEF����AB=DE��
���������������ADC�Ƕ۽�ʱ����AB=DE.
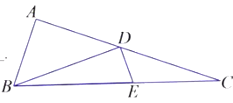
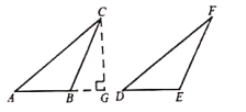
��ͼ������ABC����DEF�У�AC=DF��BC=EF����ABC=��DEF���ҡ�ABC�Ƕ۽ǣ���֤��AB=DE.
�������ɻ�����һ����Ч����ѧ˼ά��ʽ��һ���ǽ�δ���������ͨ������ת��Ϊ�ѽ��������.��Ⱥ���ֵ������������ת��Ϊ�ڶ����������ͼ������C��CG��AB��͢�����ڵ�G.
(1)����DEF���ó߹�����DE���ϵĸ�FH����д������������ͼ�ۼ���
(2)�������(1)����ͼ�Ļ����ϣ�����֤��AB=DE.
���𰸡���1������������2��������.
��������
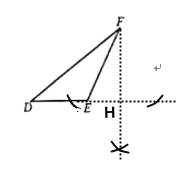
��1���߹���ͼ��FH��DE��DE�ӳ�����H���ɣ�
��2����֤����BCG����EFH,�õ�BG=EH����֤��Rt��ACG��Rt��DFH,�õ�AG=DH,Ȼ��ɵ�AB=DE.
�⣺(1)������FH����ͼ��ʾ��
��2��
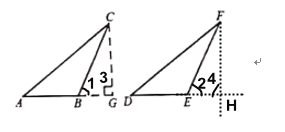
��![]() ,
,
��![]() ,
,
�֡�CG��AG��FH��DH,
��![]() ,
,
�֡�BC=EF,
����BCG����EFH,
��BG=EH��CG=FH,
�֡�AC=DF,
��Rt��ACG��Rt��DFH,
��AG=DH,
�֡�BG=EH,
��AB=DE.