题目内容
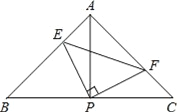
【题目】如图，已知
的平分线与
的垂直平分线相交于点
，
，
，垂足分别为
，
，
，
，则
的长为__________．
【答案】
【解析】
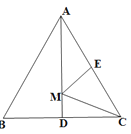
连接DC、DB，根据中垂线的性质即可得到DB=DC，根据角平分线的性质即可得到DE=DF，从而即可证出△DEB≌DFC，从而得到BE=CF，再证△AED≌△AFD，即可得到AE=AF，最后根据
，
即可求出BE.
解：如图所示，连接DC、DB，
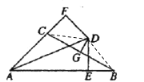
∵DG垂直平分BC
∴DB=DC
∵AD平分
，
，
∴DE=DF，∠DEB=∠DFC=90°
在Rt△DEB和Rt△DFC中，
∴Rt△DEB≌Rt△DFC
∴BE=CF
在Rt△AED和Rt△AFD中，
∴Rt△AED≌Rt△AFD
∴AE=AF
∴AB=AE＋BE=AF＋BE=AC＋CF＋BE=AC＋2BE
∵，
∴BE=
（AB－AC）=1.5.
故答案为：1.5.
练习册系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】对于抛物线
.
（1）它与x轴交点的坐标为 ，与y轴交点的坐标为 ，顶点坐标为 ；
（2）在坐标系中利用描点法画出此抛物线；
x | … | … | |||||
y | … | … |
（3）利用以上信息解答下列问题：若关于x的一元二次方程
（t为实数）在
＜x＜
的范围内有解，则t的取值范围是 ．
