题目内容
【题目】如图,在平面直角坐标系中,点A(4,0),点B(0,6),点P是直线AB上的一个动点,已知点P的坐标为(m,n).
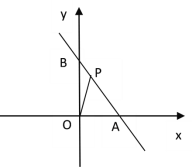
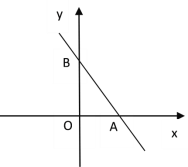
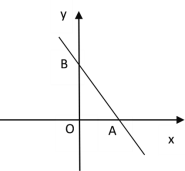
(1)当点P在线段AB上时(不与点A、B重合)
①当m=2,n=3时,求△POA的面积.
②记△POB的面积为S,求S关于m的函数解析式,并写出定义域.
(2)如果S△BOP:S△POA=1:2,请直接写出直线OP的函数解析式.(本小题只要写出结果,不需要写出解题过程).
【答案】(1)6;(2)S=3m,0<m<4;(3)y=3x或y= -3x
【解析】
(1)根据点坐标可得△POA的底和高,根据三角形面积公式计算;(2)根据点坐标可得△POB的底和高,根据三角形面积公式列出S与m的解析式;(3)分别讨论当P在第二、第一、第四象限内,根据题意列出等式求P点坐标,确定直线OP解析式.
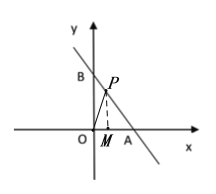
解:(1)如图,过P作PM⊥x轴,垂足为M,
∵A(4,0),P(2,3),
∴S△POA=![]() =
=![]() .
.
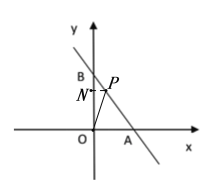
(2)如图,过P作PN⊥y轴,垂足为N,
∵B(0,6),P(m,n),
∴S =![]() =
=![]() .
.
∵P在线段AB上(不与点A、B重合)
∴0<m<4
∴S关于m的函数解析式为S=3m,0<m<4.
(3)如图,设直线AB的解析式为y=kx+b,将A(4,0),B(0,6)代入,
![]() ,
,
解得,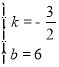 ,
,
∴直线AB的解析式为![]() ,
,
∴P(m, ![]() ).
).
∵S△BOP:S△POA=1:2,∴S△POA=2 S△BOP
①当m≤0,即点P在第二象限时,
根据题意得,![]()
解得,m= -4,
∴P(-4,12),
设直线OP解析式为y=ax,将P点代入,
-4a=12,
解得,a= -3,
∴直线OP解析式为y= -3x;
②当0<m≤4,即点P在第一象限时,
根据题意得,![]()
解得,m=![]() ,
,
∴P(![]() ,4),
,4),
设直线OP解析式为y=ax,将P点代入,
![]() a=4,
a=4,
解得,a= 3,
∴直线OP解析式为y= 3x;
③当m>4,即点P在第四象限时,
根据题意得,![]()
解得,m= -4(不符合题意,舍去) .
综上所述,直线OP的解析式为:y=3x或y= -3x


 阅读快车系列答案
阅读快车系列答案