题目内容
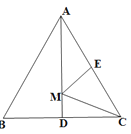
【题目】如图，等边△ABC的边长为2，AD是BC边上的中线，M是AD上的动点，E是边AC的中点，则EM+CM的最小值为( )
A.1B.12 C.3 D.
【答案】D
【解析】
根据等边三角形的性质得出AD为BC边上的垂直平分线，于是EM+CM转化为BM+EM，然后根据两点之间线段最短，推得当M'在BE和AD的交点时， EM+CM最短，最后利用勾股定理求出BE的长即可；
解：连接BE，交AD于M'，
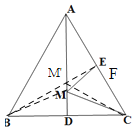
∵△ABC为等边三角形，AD为BC边上中线，
则AD⊥BC，即AD是BC的垂直平分线，
∴MB=MC，M'B=M'C，
∴ EM+CM=EM+BM，EM'+CM'=EM'+BM'，
∵EM+BM>BE=EM'+BM'，
∴当B、M、E在同一条直线上，EM+CM最小，
这时BE=
.
故答案为：D.
练习册系列答案
名校课堂系列答案
相关题目
