题目内容
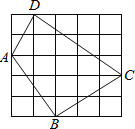
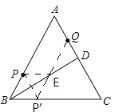
【题目】如图，等边△ABC中，BD⊥AC于点D，AD＝3.5cm，点P、Q分别为AB、AD上的两个定点且BP＝AQ＝2cm，若在BD上有一动点E使PE＋QE最短，则PE＋QE的最小值为_____cm
【答案】5
【解析】
过BD作P的对称点
,连接P，Q，Q与BD交于一点E，再连接PE，根据轴对称的相关性质以及两点之间线段最短可以得出此时PE＋QE最小，并且等于Q，进一步利用全等三角形性质求解即可.
如图，过BD作P的对称点,连接P，Q，Q与BD交于一点E，再连接PE，此时PE＋QE最小.
∵与P关于BD对称，
∴PE=E，BP=B=2cm，
∴PE＋QE= Q，
又∵等边△ABC中，BD⊥AC于点D，AD＝3.5cm，
∴AC=BC=AB=7cm，
∵BP＝AQ＝2cm，
∴QC=5cm，
∵B=2cm，
∴C=5cm，
∴△Q C为等边三角形，
∴Q=5cm.
∴PE＋QE=5cm.
所以答案为5.
练习册系列答案
相关题目
【题目】小明同学在用描点法画二次函数y=ax2+bx+c图象时，由于粗心，他算错了一个y值，列出了下面表格：
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
（1）请指出这个错误的y值，并说明理由；
（2）若点M（a，y1），N（a+4，y2）在二次函数y=ax2+bx+c图象上，且a＞﹣1，试比较y1与y2的大小．
