Question

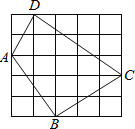
【题目】如图，小方格都是边长为1的正方形

（1）求的长度．

（2）用勾股定理的知识证明：．

Answer 1

【答案】（1）AB= ，BC= ；（2）见解析.

【解析】

（1）如图1，分别在Rt△AEB和RtBFC中分别由勾股定理可求得AB和BC的长；
（2）如图2，连接AC，在Rt△ACG中由勾股定理可求得AC，则可得到AB2+BC2=AC2，可证得△ABC为直角三角形，即可得结论．

(1) 解：如图1，

在Rt△ABE中，AE=3，BE=2，

∴AB= = ，

在Rt△BCF中，BF=3，CF=2，

∴BC= = ；

(2)证明：如图2，连接AC，

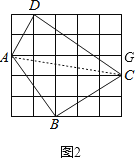
在Rt△ACG中，AG=5，CG=1，

∴AC= ，

结合(1)可得 =

∴△ABC是以AC为斜边的直角三角形，

∴∠ABC=90°.

故答案为：（1）AB= ，BC= ；（2）见解析.