题目内容
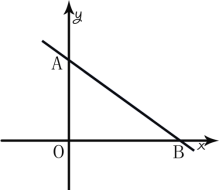
【题目】如图，直线MN与x轴、y轴分别相交于B、A两点，OA,OB的长满足式子
(1)求A，B两点的坐标;
(2)若点O到AB的距离为
，求线段AB的长；
（3）在（2）的条件下，x轴上是否存在点P,使ΔABP使以AB为腰的等腰三角形，若存在请直接写出满足条件的点P的坐标.
【答案】 (1) A(0，6)B(8，0)；（2）
；（3）存在，（-8,0）、（-2,0）、（18,0）.
【解析】
（1）根据非负数的性质可得OA=6、OB=8，即可求得A、B两点的坐标；（2）根据直角三角形面积的两种表示法即可求得AB的长；（3）分AB=B P1、AB=A P2、AB=B P3三种情况求点P的坐标.
（1）∵
，
∴OA=6，OB=8，
∴A(0，6)，B(8，0)；
（2）∵
，
∴AB=10；
（3）在x轴上存在点P，是使ΔABP使以AB为腰的等腰三角形，点P的位置如图所示，
①当AB=BP1时，P1的坐标为（18，0）；②当AB=AP2时，P2的坐标为（-8，0）；③当AB=BP3时，P3的坐标为（-2，0）.
练习册系列答案
相关题目
【题目】一次学科测验，学生得分均为整数，满分10分，成绩达到6分以上为合格．成绩达到9分为优秀．这次测验中甲乙两组学生成绩分布的条形统计图如下：
（1）请补充完成下面的成绩统计分析表：
平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
甲组 | 6.9 | 2.4 | 91.7% | 16.7% | |
乙组 | 1.3 | 83.3% | 8.3% |
（2）甲组学生说他们的合格率、优秀率均高于乙组，所以他们的成绩好于乙组．但乙组学生不同意甲组学生的说法，认为他们组的成绩要高于甲组．请你给出三条支持乙组学生观点的理由．
