题目内容
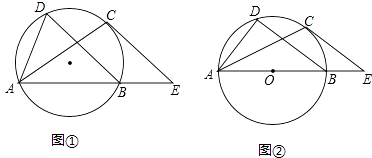
【题目】[发现]如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)
(1)[思考]如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A, B,C三点的圆上吗?
(2)我们知道,如果点D不在经过A,B,C三点的圆上,那么点D要么在圆O外,要么在圆O内,以下该同学的想法说明了点D不在圆O外。
请结合图④证明点D也不在⊙O外.

[结论]综上可得结论:如图②,如果∠ACB=∠ADB=a(点C,D在AB的同侧),那么点D在经过A,B,C三点的圆上,即:点A、B、C、D四点共圆。
[应用]利用上述结论解决问题:
如图⑤,已知△ABC中,∠C=90°,将△ACB绕点A顺时针旋转一个角度得△ADE,连接BE CD,延长CD交BE于点F,
图⑤
①求证:点B、C、A、F四点共圆;②求证:BF=EF.
【答案】
(1)如图,假设点D在⊙O内,延长AD交⊙O于点E,连接BE;则∠AEB=∠ACB
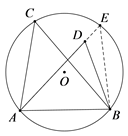
∵∠ADB是△DBE的一个外角
∴∠ADB>∠AEB
∴∠ADB>∠ACB
这与条件∠ACB=∠ADB矛盾
∴点D不在⊙O内
(2)①证明:∵AC=AD,AB=AE,
∴∠ACD=∠ADC,∠ABE=∠AEB,
∵∠CAB=∠DAE,
∴∠CAD=∠BAE,
∵2∠ACD+∠CAD=180°,2∠ABE+∠BAE=180°,
∴∠ACD=∠ABE,
∴B、C、A、F四点共圆
②证明:∵B、C、A、F四点共圆,
∴∠BFA+∠BCA=180°,
∵∠ACB=90°,∴∠BFA=90°,
∴AF⊥BE,
∵AB=AE,
∴BF=EF
【解析】利用已知的结论,四边形的两对角线所分四个内角所成的8个角中,若所对同一条边的两个角相等,则这个四边形内接于圆,再结合旋转的性质,得出一对角相等即可.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如表
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
下列结论:
①ac<0; ②当x>1时,y的值随x值的增大而减小;
③当 ![]() 时,
时, ![]() ; ④3是方程ax2+(b﹣1)x+c=0的一个根.
; ④3是方程ax2+(b﹣1)x+c=0的一个根.
其中正确的结论是(填正确结论的序号).