题目内容
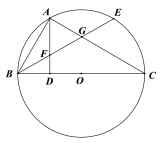
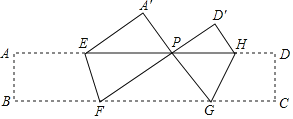
【题目】已知:如图,AB为![]() 的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
的直径,点C是半圆上一点,CE⊥AB于E,BF∥OC,连接BC,CF.
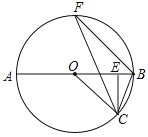
(1)求证:∠OCF=∠ECB;
(2)当AB=10,BC=![]() ,求CF的值.
,求CF的值.
【答案】(1)证明见详解.
(2)![]()
【解析】
(1)延长CE交⊙O于点G,利用圆周角的性质进行解答即可.
(2)连接AC,FO,利用△AOC和△FOC均是等腰三角形并且全等,得到CF=AC,在根据AB为直径,△ABC为直角三角形,利用勾股定理求出AC即可得到CF的长.
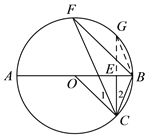
证明:(1)延长CE交⊙O于点G.
∵AB为⊙O的直径,CE⊥AB于E,
∴BC=BG,
∴∠G=∠2,
∵BF∥OC,
∴∠1=∠F,
又∵∠G=∠F,
∴∠1=∠2.
即∠OCF=∠ECB.
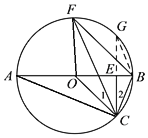
(2)连接AC,FO
∴OA=OC=OF,∠A=∠CFB,
由(1)可知∠1=∠CFB,并△AOC和△FOC均是等腰三角形
∴∠1=∠OFC=∠A=∠ACO
在△AOC和△FOC中
OC是公共边,∠1= =∠ACO,∠OFC=∠A
∴△AOC![]() △FOC
△FOC
∴CF=AC
∵AB为直径
∴![]()
∴![]()
![]()

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
【题目】对某校学生寒假阅读时间情况调查,抽样统计绘制了两幅不完整的统计图,请结合信息解决下列问题:
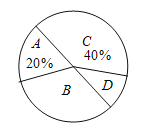
阅读时间(小时) |
|
|
|
|
人数 | 60 | 80 |
(1)这次统计A类 人;D类 人;
(2)如果该校有1200学生,那么D类学生数量约为多少人?
(3)甲、乙、丙、丁4名学生是阅读属于D类学生,他们分别来自九年级1人,八年级1人,七年级2人,现抽取2人电话回访,则抽取到2人同为七年级学生的概率为多少?