题目内容
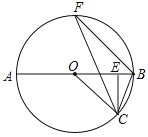
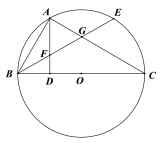
【题目】如图,BC是⊙O的直径,点A在⊙上,AD⊥BC,垂足为D,![]() ,BE分别交AD、AC与点F、G.
,BE分别交AD、AC与点F、G.
(1)证明:FA=FB.
(2)BD=DO=2,求弧EC的长度.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)根据BC是⊙O的直径,AD⊥BC,![]() ,推出∠ABE=∠BAD,即可推得FA=FB.
,推出∠ABE=∠BAD,即可推得FA=FB.
(2)根据BD=DO=2,AD⊥BC,求出∠AOB=60°,再根据![]() ,求出∠EOC=60°,即可求出弧EC的长度是多少.
,求出∠EOC=60°,即可求出弧EC的长度是多少.
(1)证明:∵BC是⊙O的直径,
∴∠BAC=90°,
∴∠BAD+∠CAD=90°;
又∵AD⊥BC,
∴∠C+∠CAD=90°;
∴∠BAD=∠C,
∵![]() ,
,
∴∠C=∠ABE,
∴∠BAD=∠ABE
∴ FA=FB;
(2)连接OA、OE.
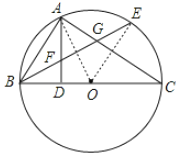
∵BD=DO=2,AD⊥BC,
∴AB=AO,
∵AO=BO,
∴ AB=OA=OB=4
∴ △OAB是等边三角形,
∴∠AOB=60°,
∵![]() ,
,
∴∠AOE=60°,
∴ ∠EOC=60°
∴弧EC的长为:![]() .
.

练习册系列答案
相关题目