ƒøƒ⁄»ð
°æƒø°ø∂‘ƒ≥–£—ß…˙∫ƺŸ‘ƒ∂¡ ±º‰«Èøˆµ˜≤È£¨≥È—˘Õ≥º∆ªÊ÷∆¡À¡Ω∑˘≤ªÕÍ’˚µƒÕ≥º∆Õº£¨«ÎΩ·∫œ–≈œ¢Ω‚戜¬¡–Œ £∫
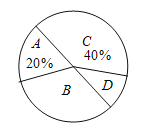
‘ƒ∂¡ ±º‰£®–° ±£© |
|
|
|
|
»À ˝ | 60 | 80 |
£®1£©’‚¥ŒÕ≥º∆A¿ý »À£ªD¿ý »À£ª
£®2£©»Áπ˚∏√–£”–1200—ß…˙£¨ƒ«√¥D¿ý—ß…˙ ˝¡ø‘ºŒ™∂ý…Ÿ»À£ø
£®3£©º◊°¢““°¢±˚°¢∂°4√˚—ß…˙ «‘ƒ∂¡ Ù”⁄D¿ý—ß…˙£¨À˚√«∑÷±¿¥◊‘æ≈ƒÍº∂1»À£¨∞ÀƒÍº∂1»À£¨∆þƒÍº∂2»À£¨œ÷≥È»°2»ÀµÁª∞ªÿ∑√£¨‘Ú≥È»°µΩ2»ÀÕ¨Œ™∆þƒÍº∂—ß…˙µƒ∏≈¬ Œ™∂ý…Ÿ£ø
°æ¥∞∏°ø£®1£©40£¨20£ª£®2£©120»À£ª£®3£©![]()
°æΩ‚Œˆ°ø
£®1£©“—÷™C¿ý—ß…˙’º40%«“”–80»À£¨ø…÷™◊лÀ ˝£¨‘Ÿ∏˘æðA¿ý£¨D¿ýÀ˘’º∞Ÿ∑÷±»«Ûµ√»À ˝.
£®2£©∏˘æðB¿ýÀ˘”–»À ˝∫Õ“—«Û≥ˆµƒ◊лÀ ˝£¨µ√≥ˆB¿ýÀ˘’º∞Ÿ∑÷±»£¨º¥ø…«Û≥ˆDÀ˘’º∞Ÿ∑÷±»£¨‘Ÿ≥À“‘◊лÀ ˝£¨º¥ø…«Û≥ˆD¿ý—ß…˙ ˝¡ø‘ºŒ™∂ý…Ÿ.
£®3£©¿˚”√Àʪ˙ ¬º˛∏≈¬ µƒ∑Ω∑®£¨º◊°¢““°¢±˚°¢∂°À˚√«∑÷±¿¥◊‘æ≈ƒÍº∂1»À£¨∞ÀƒÍº∂1»À£¨∆þƒÍº∂2»À£¨œ÷≥È»°2»ÀµÁª∞ªÿ∑√£¨π≤”–∂ý…Ÿ÷÷«Èøˆ£¨≥È»°Õ¨ «∆þƒÍº∂—ß…˙ø…ƒÐ”–º∏÷÷«Èøˆ£¨œý±»µ√∏≈¬ .
£®1£©“—÷™C¿ý—ß…˙’º40%«“”–80»À£¨◊лÀ ˝![]() »À
»À
A¿ý»À ˝Œ™£∫20020%=40»À
D¿ý»À ˝£∫200-40-60-80=20»À
π ¥∞∏£∫40£ª20
£®2£©B¿ýÀ˘’º◊лÀ ˝µƒ∞Ÿ∑÷±»Œ™£∫![]()
ø…µ√D¿ýÀ˘’º◊лÀ ˝µƒ∞Ÿ∑÷±»Œ™£∫1-£®20%+30%+40%£©=10%
»Á∏√–£”–1200—ß…˙£¨ƒ«√¥D¿ý—ß…˙»À ˝Œ™£∫120010%=120»À
π ¥∞∏£∫120»À
£®3£©¿˚”√Àʪ˙ ¬º˛∏≈¬ µƒ∑Ω∑®£¨º◊°¢““°¢±˚°¢∂°À˚√«∑÷±¿¥◊‘æ≈ƒÍº∂1»À£¨∞ÀƒÍº∂1»À£¨∆þƒÍº∂2»À£¨œ÷≥È»°2»ÀµÁª∞ªÿ∑√£¨π≤”–12÷–«Èøˆ£¨≥È»°µƒ¡Ω√˚—ß…˙Õ¨ «∆þƒÍº∂µƒ”–¡Ω÷÷«Èøˆ£¨π ≥È»°µΩ2»ÀÕ¨Œ™∆þƒÍº∂—ß…˙µƒ∏≈¬ Œ™![]()
π ¥∞∏£∫![]()

 ΩÃ≤ƒ»´Ω‚◊÷¥ æ‰∆™œµ¡–¥∞∏
ΩÃ≤ƒ»´Ω‚◊÷¥ æ‰∆™œµ¡–¥∞∏