题目内容
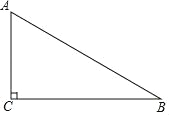
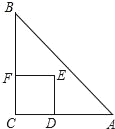
【题目】如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
A. 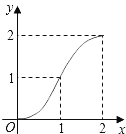 B.
B. 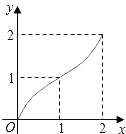
C. 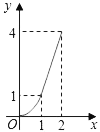 D.
D. 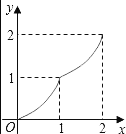
【答案】A
【解析】
当0<x≤1时,根据正方形的面积公式得到y=x2;当1<x≤2时,ED交AB于M,EF交AB于N,利用重叠的面积等于正方形的面积减去等腰直角三角形MNE的面积得到y=x2﹣2(x﹣1)2,配方得到y=﹣(x﹣2)2+2,然后根据二次函数的性质对各选项进行判断.
解:当0<x≤1时,y=x2,
当1<x≤2时,ED交AB于M,EF交AB于N,如图,
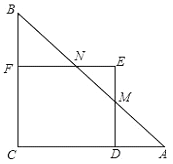
CD=x,则AD=2﹣x,
∵Rt△ABC中,AC=BC=2,
∴△ADM为等腰直角三角形,
∴DM=2﹣x,
∴EM=x﹣(2﹣x)=2x﹣2,
∴S△ENM=![]() (2x﹣2)2=2(x﹣1)2,
(2x﹣2)2=2(x﹣1)2,
∴y=x2﹣2(x﹣1)2=﹣x2+4x﹣2=﹣(x﹣2)2+2,
∴y=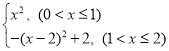 ,
,
故选A.

练习册系列答案
相关题目
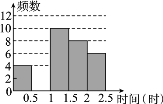
【题目】某中学对本校初中学生完成家庭作业的时间做了总量控制,规定学生每天完成家庭作业的时间少于1.5小时.该校数学课外兴趣小组对本校初中学生回家完成作业的时间作了一次随机抽样调查,并绘制出频数分布表和频数分布直方图的一部分.
时间(时) | 频数 | 频率 |
0≤t<0.5 | 4 | 0.1 |
0.5≤t<1 | a | 0.3 |
1≤t<1.5 | 10 | 0.25 |
1.5≤t<2 | 8 | b |
2≤t<2.5 | 6 | 0.15 |
合计 | 1 |
(1)在频数分布表中,a=________,b=________;
(2)补全频数分布直方图;
(3)请估计该校1400名初中学生中,有多少名学生在1.5小时以内(不包括1.5小时)完成了家庭作业?![]()